Предмет: Алгебра,
автор: calvinkleinn
Вычислить интеграл) заранее спасибо))
Приложения:
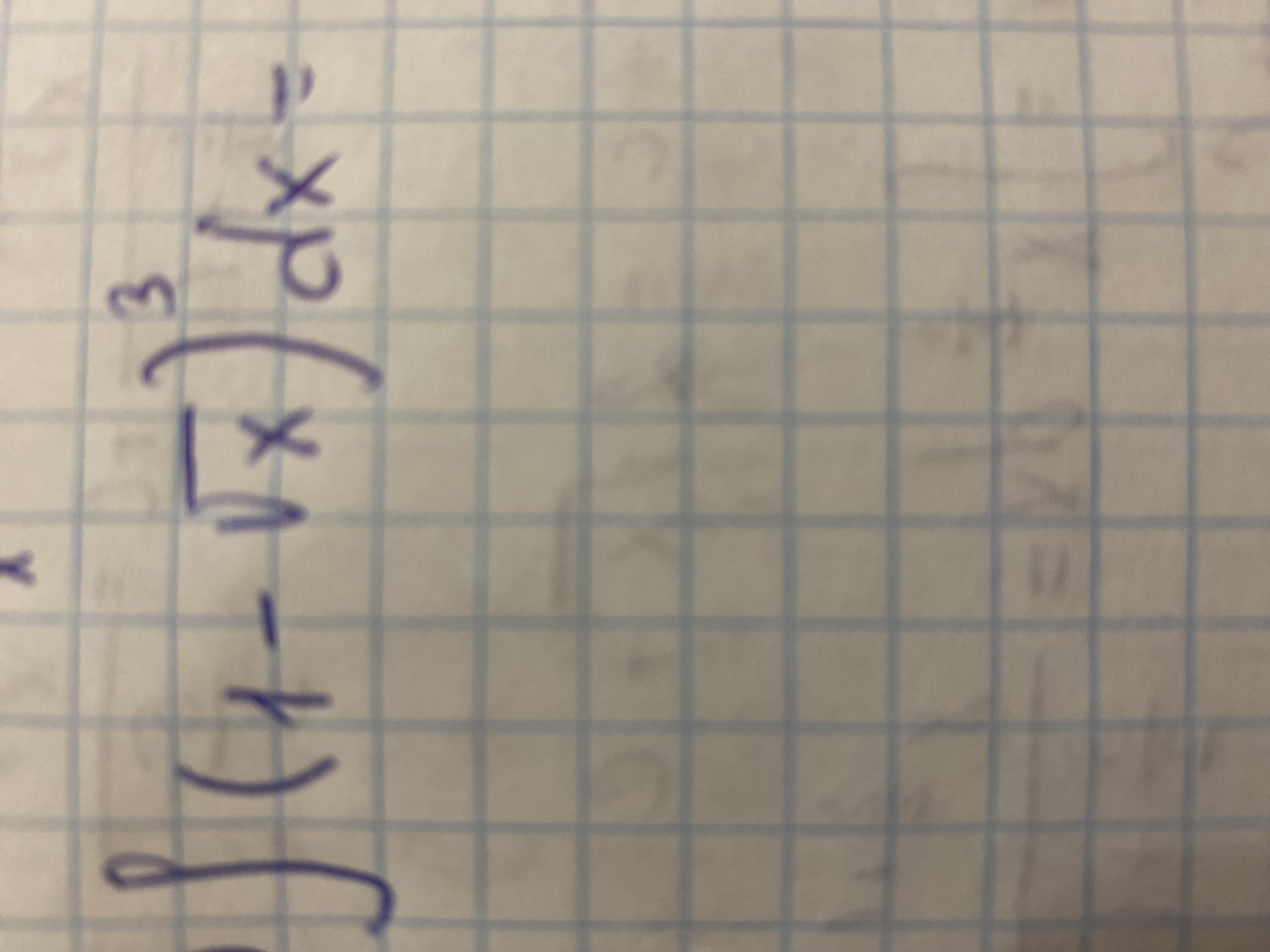
Ответы
Автор ответа:
1
∈
;
***выражение
Простите
Что Вы, не извиняйтесь. Я уверен, Вы просто допустили опечатку или случилось что-то подобное. Мы люди, все мы ошибаемся маленько ))
Автор ответа:
1
=∫(1-3√х+3х-х³/²)dx=х-(2х³/²)/3+3х₂/2-(2/5)х⁵/²+с
Похожие вопросы
Предмет: Другие предметы,
автор: NickiNott
Предмет: Українська мова,
автор: vadimpaladiuch
Предмет: Русский язык,
автор: erik99
Предмет: Математика,
автор: prostoDimka000
Предмет: Алгебра,
автор: MrBloody15
∫(3*√(x))dx = ∫(3*(x^(1/2)))dx = 2*x^(3/2) = 2*x*√(x)
Легко проверить через выражения производной от 2*x*√(x):
(2*x*√(x))' = (2*x^(3/2))' = 2*(3/2)*x^((3/2)-1) = 3*x^(1/2) = 3*√(x)