Предмет: Математика,
автор: Luminescence
Помогите пожалуйста с примером
Найдите интеграл, используя интегрирование по частям:
Приложения:
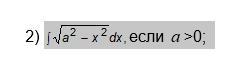
Ответы
Автор ответа:
1
Ответ:
Пошаговое объяснение:
Для формулы интегрирования по частям возьмем
Подставляя в формулу, получаем:
Преобразуем интеграл в правой части:
Последний интеграл есть табличный:
Обозначим искомый интеграл как тогда получаем уравнение относительно
:
Luminescence:
Спасибо большое!
Похожие вопросы
Предмет: Русский язык,
автор: akylbaeva2000
Предмет: Английский язык,
автор: vitaliyhrustov
Предмет: Українська мова,
автор: fetsovitch
Предмет: Геометрия,
автор: Тася566
Предмет: Химия,
автор: taniushamik