Предмет: Математика,
автор: PAIN1999
Исследуйте на сходимость ряд:
Приложения:
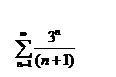
Аноним:
используйте признак Даламбера
Ответы
Автор ответа:
1
Ответ: ряд расходится.
Пошаговое объяснение:
1) Составляем выражение для n+1 - го члена: a(n+1)=3^(n+1)/(n+2)=3*3^n/(n+2).
2) Составляем отношение n+1 - го члена к n - му: a(n+1)/a(n)=3*(n+1)/(n+2).
3) Находим предел этого отношения при n⇒∞: он равен 3>1, поэтому по признаку Даламбера ряд расходится.
Вообще говоря, здесь можно обойтись и без признака Даламбера. Так как при любом n 3^n>n+1, то a(n) при n⇒∞ не стремится к нулю, а это достаточный признак расходимости ряда.
А почему в пункте 1 умножается 3 на 3, то есть как к этому пришли? И если можете объяснить, то скажите поподробней процесс 2 пункта, откуда числа по
Допишу: появились
Похожие вопросы
Предмет: Русский язык,
автор: polyubinatatya
Предмет: Русский язык,
автор: belousov2005qwe
Предмет: Русский язык,
автор: bagira014
Предмет: Математика,
автор: МСкотопес
Предмет: Математика,
автор: Алиса00000000