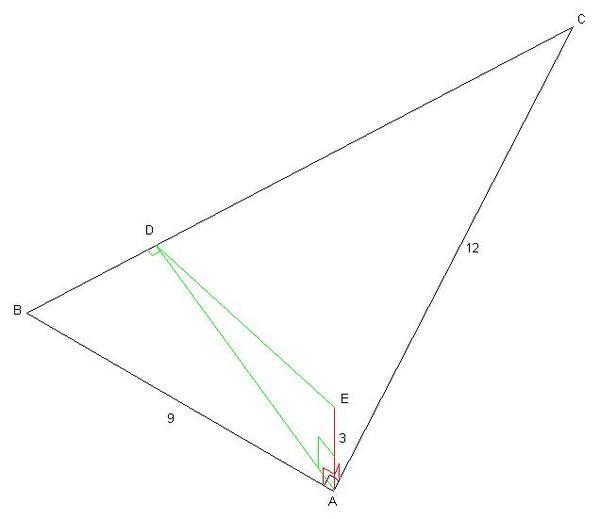
Катети прямокутного трикутника дорівнюють 9см і 12см. У вершині прямого кута побудовано перпендикуляр до площини трикутника завдовжки 3см. Знайти відстані від кінців перпендикуляра до гіпотенузи. DA. це катет прямокутного трикутника ADE. Другий катет відомий, знаходиш гіпотенузу DE.
Ответы
"Катеты прямоугольного треугольника равны 9см и 12см. В вершине прямого угла построен перпендикуляр к плоскости треугольника длиной 3см. Найти расстояния от концов перпендикуляра до гипотенузы. DA. это катет прямоугольного треугольника ADE. Второй катет известен, находишь гипотенузу DE."
Объяснение:
Расстоянием от А до СВ , будут АD, т.к АD⊥BС.
Расстоянием от Е до СВ , будут ЕD, т.к ЕD⊥BС по т. о трех перпендикуляра: если проекция АD перпендикулярна прямой лежащей в плоскости ВС, то и наклонная ЕD перпендикулярна ВС. .
1) ΔАВС-прямоугольный, по т. Пифагора СВ=√(9²+12²)=√225=15 (см).
По т. о среднем пропорциональном АС²=СD*СВ⇒ СD=144:15=9,6(см).
ΔАСD-прямоугольный , по т. Пифагора АD=√(12²-9,6²)=7,2 (см).
2)ΔАЕD-прямоугольный , по т. Пифагора ЕD=√(3²+7,2²)=7,8 (см).