Предмет: Математика,
автор: kiemitak
15Б. СРОЧНО!!!Исследовать сходимость знакочередующегося ряда и установить характер сходимости:
Приложения:
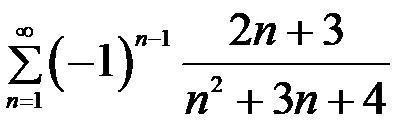
Ответы
Автор ответа:
2
Так как сам ряд является сходящимся, а модуль ряда расходится то исходный ряд сходится условно.
kiemitak:
ты мой спаситель, спасибо :*
Похожие вопросы
Предмет: Русский язык,
автор: meste
Предмет: Русский язык,
автор: sveta3853
Предмет: Русский язык,
автор: dvda
Предмет: Алгебра,
автор: seriy2003
Предмет: Математика,
автор: 2007jnis