Предмет: Алгебра,
автор: michattr
помогите решить СРОЧНО!
(спасибо)
Приложения:
Ответы
Автор ответа:
1
Ответ:
Объяснение:
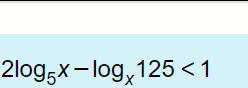
2log_5x-log_x125<1
ОДЗ:
x>0
x1
Тогда:
2log_5x-3log_x5<1
2log_5x-3×1/log_5x<1
Замена: t=log_5x
2t-3/t-1<0
(2t²-t-3)/t<0
(2t²+2t-3t-3)/t<0
(2t(t+1)-3(t+1))/t<0
((t+1)(2t-3))/t<0
t<-1 и 0<t<3/2
С учетом замены:
t<-1
log_5x<-1
a=5>1 =>
x<1/5
0<log_5x<3/2
log_5x>0
a=5>1 =>
x>1
log_5x<3/2
a=5>1 =>
x<
C учетом ОДЗ:
Похожие вопросы
Предмет: Русский язык,
автор: KirillZiZ
Предмет: Другие предметы,
автор: MsKiss
Предмет: Русский язык,
автор: Янтарик
Предмет: История,
автор: Emperator2017
Предмет: Геометрия,
автор: Маадыр