Предмет: Математика,
автор: dromaneyko
Найти интервалы возрастания и убывания функции y=2x^3-3x^2-36x+ 40.
dnepr1:
Зачем одна и та же функция дважды записана???
А не могли бы вы решить это
Найти интервалы возрастания и убывания функции y=x^3-4x^2+4x
А что мешает по готовому образцу самому решить???
Ответы
Автор ответа:
2
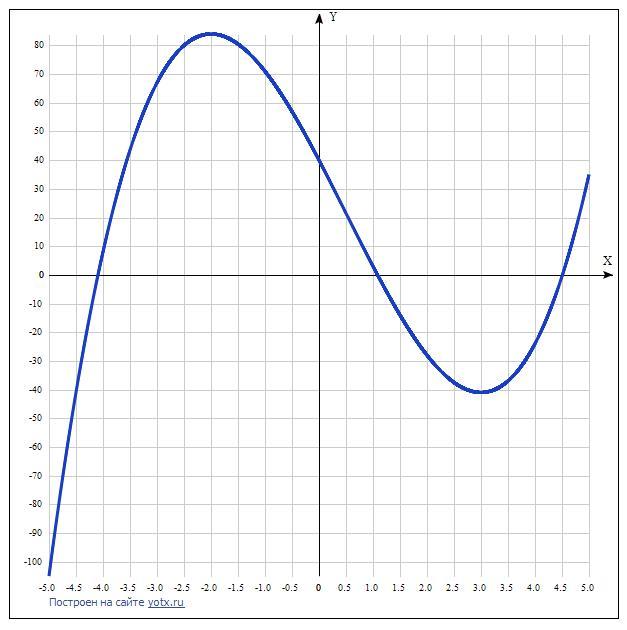
Дана функция y=2x^3-3x^2-36x+ 40.
Находим её производную.
y' = 6x² - 6x - 36.
Приравниваем производную нулю.
6x² - 6x - 36 = 6(x² - x - 6) = 0. Находим корни квадратного трёхчлена
x² - x - 6 = 0. D = 1 - 4*1*(-6) = 25. √D = +-5.
x1 = (1 - 5)/2 = -2, x2 = (1 + 5)/2 = 3.
Найдены критические точки x1 = -2 и x2 = 3.
Имеем 3 промежутка монотонности функции.
Находи знаки производной на этих промежутках.
х = -3 -2 0 3 4
y' = 36 0 -36 0 36 .
Как видим. на промежутках (-∞; -2) и (3; +∞) функция возрастает,
на промежутке (-2; 3) функция убывает.
Приложения:
Похожие вопросы
Предмет: Русский язык,
автор: Лиза5666
Предмет: Русский язык,
автор: 1xXxdenisxXx1
Предмет: Русский язык,
автор: Олюнчик1
Предмет: Математика,
автор: Аноним
Предмет: Музыка,
автор: Аноним