Предмет: Геометрия,
автор: lilforky
Реши тригонометрическое уравнение 5sin2x+11sinx=12 .
Приложения:

Ответы
Автор ответа:
2
На фото решение. Прикрепил Вам скриншот с правильными ответами:
Приложения:

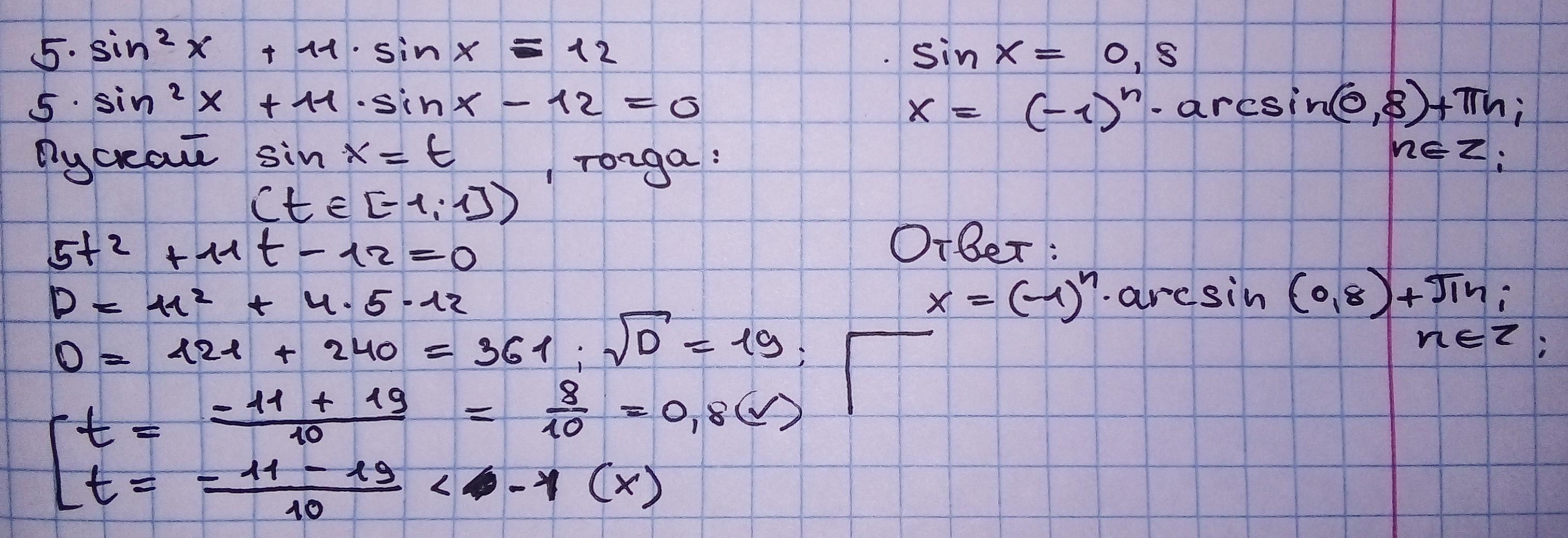
Автор ответа:
0
Ответ: №1 и №3 .
Похожие вопросы
Предмет: Русский язык,
автор: kristina20026
Предмет: Русский язык,
автор: elenamarusya74
Предмет: Русский язык,
автор: Фаолан
Предмет: Алгебра,
автор: AshotHookshot
Предмет: Информатика,
автор: Оля123315