Предмет: Математика,
автор: adeleks00
вычислить несобственный интеграл
Приложения:
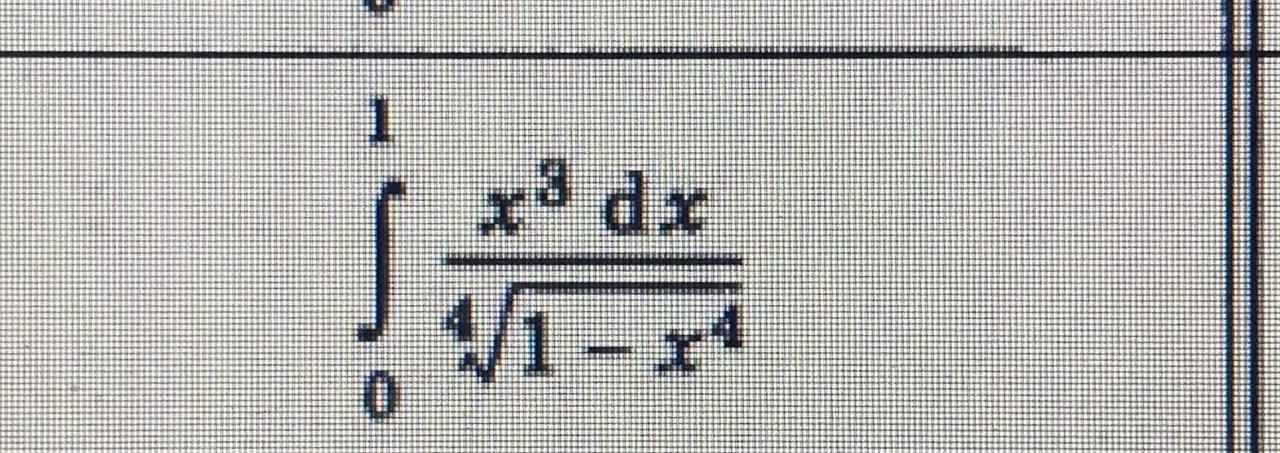
Ответы
Автор ответа:
1
Ответ:
Пошаговое объяснение:
(в скобках пределы интегрирования)
Похожие вопросы
Предмет: Русский язык,
автор: 2002MARK
Предмет: Русский язык,
автор: coni2005
Предмет: Английский язык,
автор: myslivanjan
Предмет: Математика,
автор: крисс3500