Question

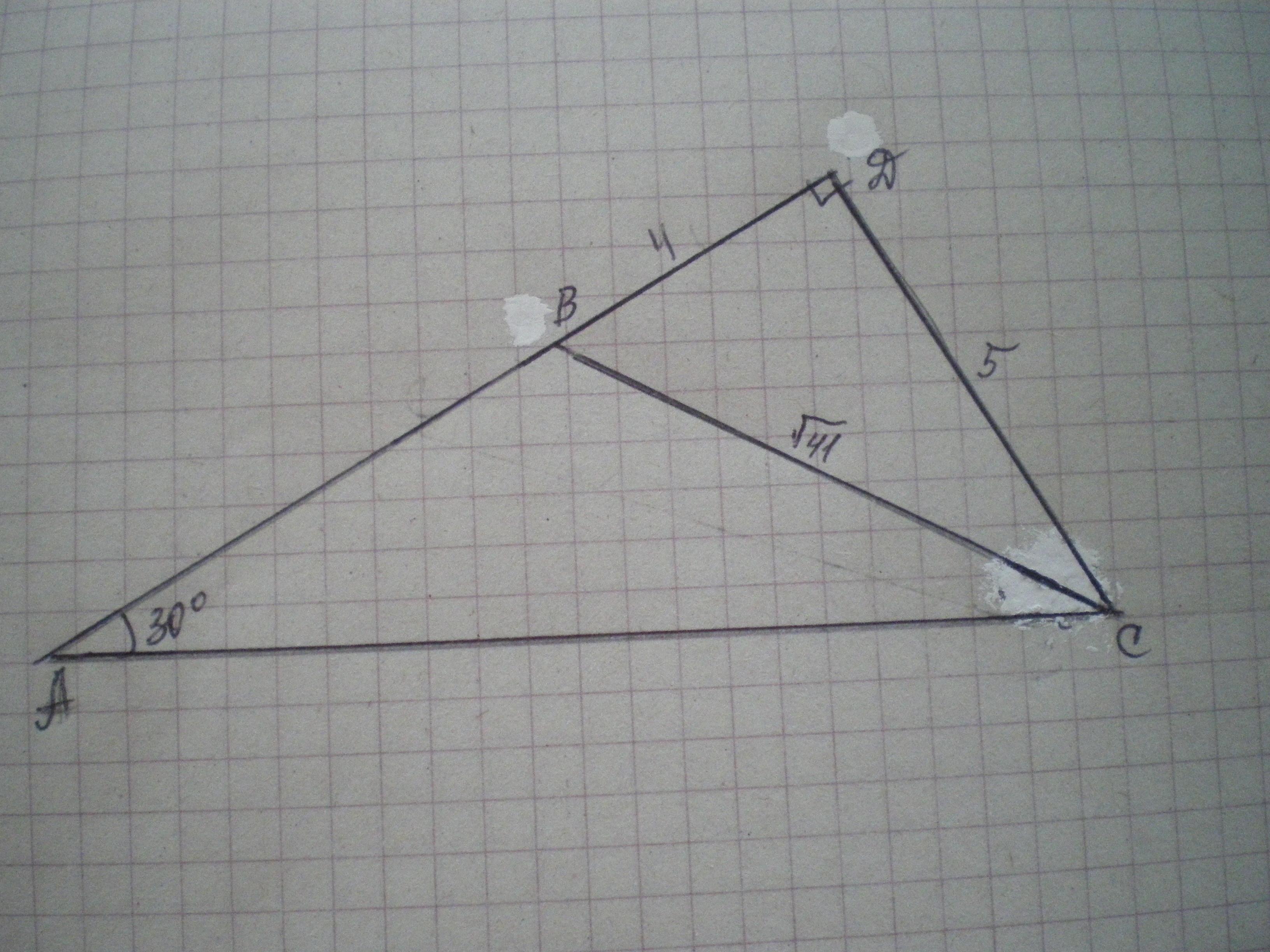
Дан треугольник ABC. А=30° и BC=√41см. Из вершины С к стороне АВ проведена высота СD,длина которой 5 см. Найди сторону АВ.

Answer 1

Ответ:

(5√3)-4 см.

Пошаговое объяснение:

Дано: ΔАВС, ∠А=30°, ВС=√41 см, СD - высота, СD=5 см. Найти АВ.

В данном треугольнике высота СD падает на продолжение стороны АВ, таким образом имеем ΔАСD - прямоугольный, ∠D=90°.

Катет СD лежит против угла 30°, поэтому он равен половине гипотенузы АС, тогда АС=2СD=10 см.

Найдем АD по теореме Пифагора:

АD=√(АС²-СD²)=√(100-25)=√75 =5√3 см.

АВ=АD-ВD, поэтому найдем ВD из ΔВDС

ВD²=ВС²-СD²=41-25=16;  ВD=4 см.

АВ=(5√3)-4 см.