Предмет: Алгебра,
автор: vanserebro
Помогите решить, пожалуйста
Приложения:
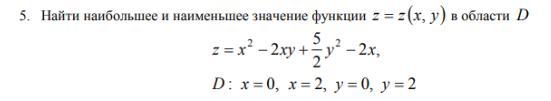
Ответы
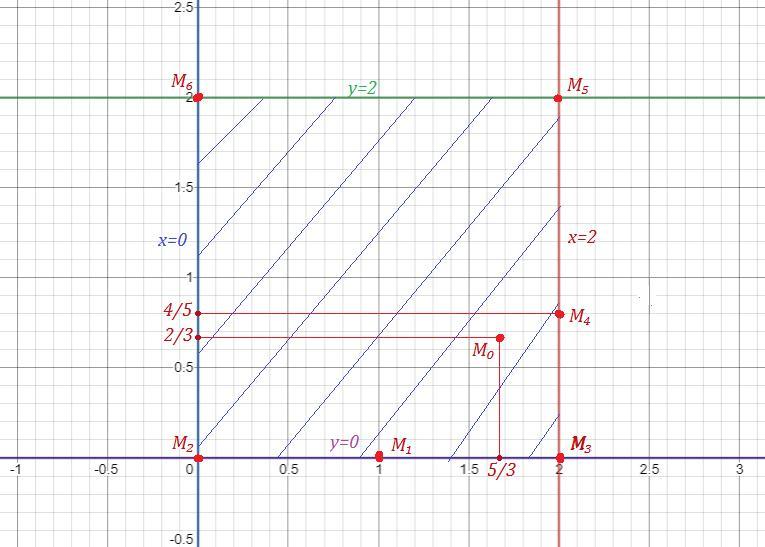
Автор ответа:
0
Приложения:
Похожие вопросы
Предмет: Русский язык,
автор: rassomagina
Предмет: Русский язык,
автор: lenaborisovna
Предмет: Английский язык,
автор: sidyakinal1984
Предмет: Математика,
автор: stepak668