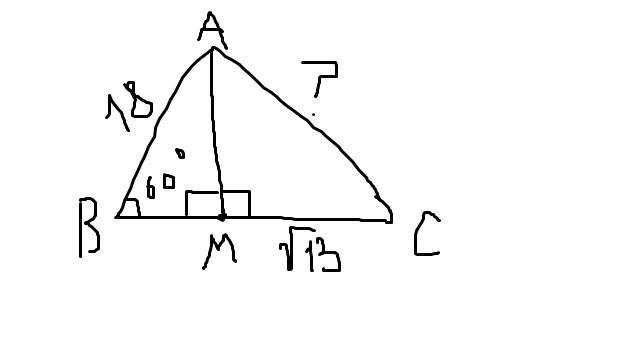
Высота АМ делит сторону ВС треугольника АВС на отрезки ВМ и СМ.
Найдите сторону АС, если СМ = √13 см, угол АВС равен 60, а сторона АВ
равна 18 см.
Ответы
Решение:
Рисунок, как должно быть, я тебе прикрепила.
Смотри.
Высота, проведённая к основанию образовала прямой угол. Получилось 2-ва прямоугольных треугольника.
У нас есть угол B, (ABC), который равен 60 градусам, есть сторона AB, которая равна 18 см.
Мы можем найти угол BAM, 90+60=150 и 180-150=30 (т.к сумма углов в треугольнике равна 180)
А как мы знаем, на против угла в 30 градусов лежит катет, равный половине гипотенузы), т.е BM=18/2=9 см.
Теперь мы можем найти высоту AM. Это катет.
По теореме Пифагора:
AM²=BA²-BM² (подставляем числа)
AM²=18²-9²
Считаем и получаем, что AM=√243=9√3
Знаем, что высота равна 9√3, MC=√13, нам нужно найти гипотенузу AC.
По теореме Пифагора:
AC²=AM²+MC² (подставляем числа):
AC²=243+13 (складываем и под корень возводим их сумму)
AC²=√256
AC=16 см
Ответ: AC=16 см.
На самом деле, эту задачу можно бы было решить не через угол в 30°, а через синус угла 60°, я сначала так и поступила, но тебе я написала лёгкий вариант решения этой задачи.