Предмет: Геометрия,
автор: ilakrasnogrudov
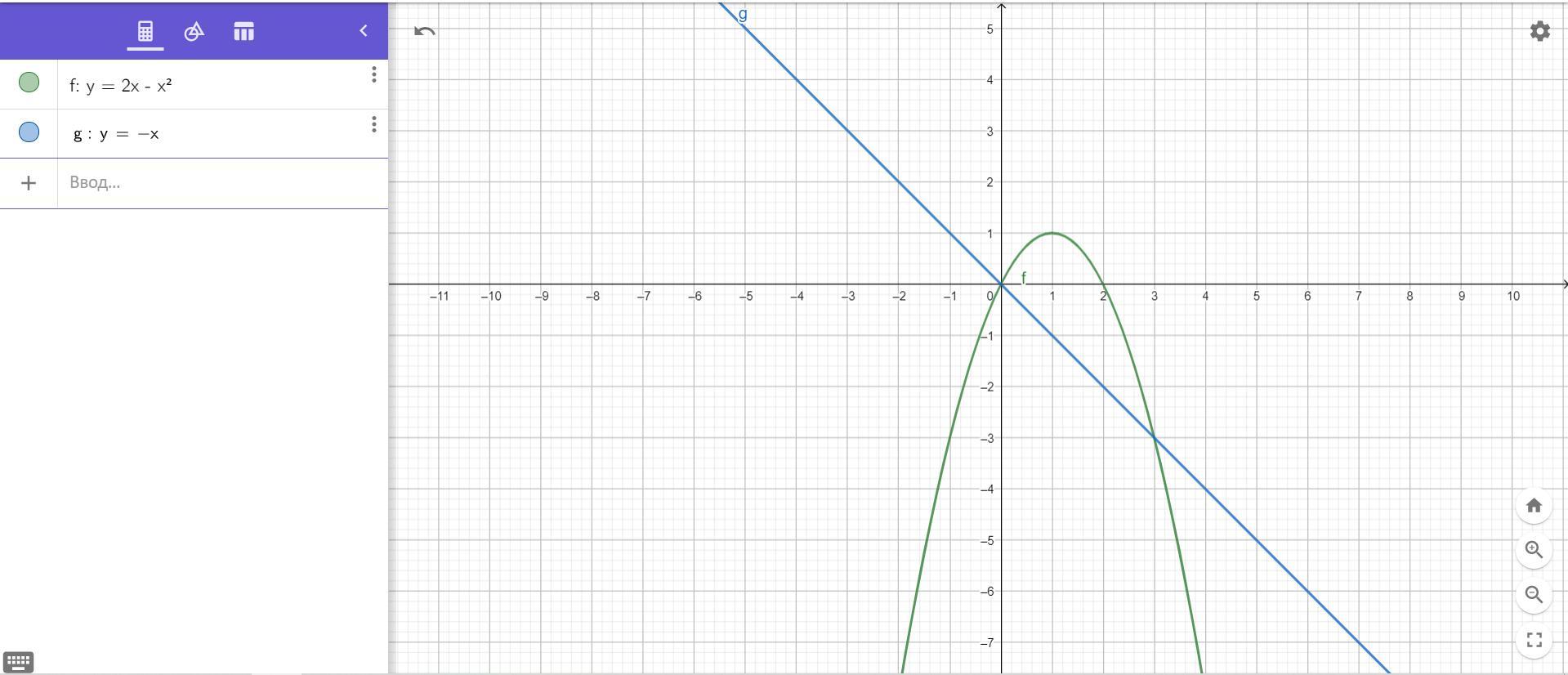
Найти площадь фигуры, ограниченной кривыми
y=2x-x^2 и x+y=0
Ответы
Автор ответа:
0
Приложения:
Похожие вопросы
Предмет: Другие предметы,
автор: dmitrychupin
Предмет: Русский язык,
автор: mart1979
Предмет: Русский язык,
автор: KenNyaa12
Предмет: Химия,
автор: irinaakulina
Предмет: Геометрия,
автор: katerina300