Предмет: Алгебра,
автор: kaikmer1
Помогите решить задачу. Уже 3 часа сижу туплю
Приложения:
Ответы
Автор ответа:
1
Чтобы вычислить площадь фигуры, ограниченной графиком функции на заданном промежутке
, следует найти определенный интеграл:
где — первообразная для функции
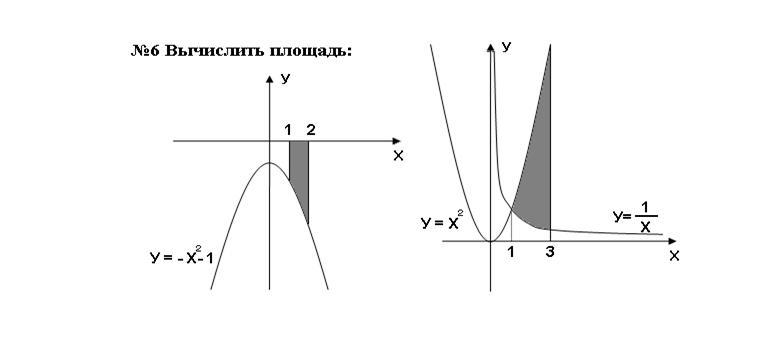
1) Имеем функцию и следует вычислить площадь, которую она ограничивает на координатной плоскости на отрезке
Найдем определенный интеграл, приписав перед ним знак "минус", поскольку график функции находится под осью абсцисс:
2) Вычислим площадь фигуры, ограниченной графиками функций и
на отрезке
Чтобы найти эту площадь, следует вычислить определенный интеграл разности функций и
(только при такой разности площадей, образованных функциями на координатной плоскости, получим площадь фигуры, изображенной на рисунке):
Ответ: 1) кв. ед.; 2)
кв. ед.
Автор ответа:
2
Ответ:
Объяснение:
!!!!!!!!!!!!!!!!!!!!!
Приложения:
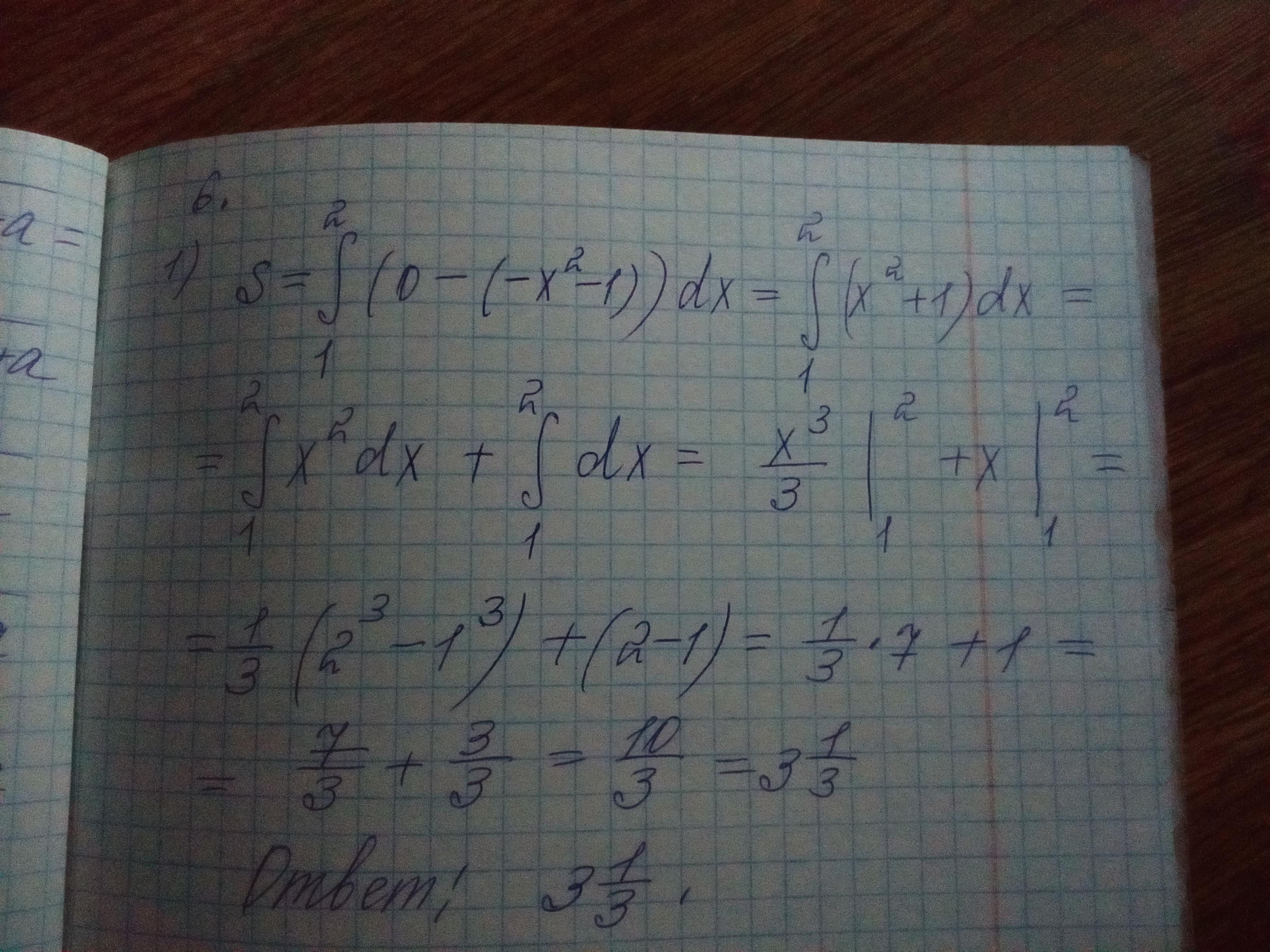
m11m:
Решение второго задания смотрите у Nikebod313.
Похожие вопросы
Предмет: Другие предметы,
автор: JeevasM
Предмет: Русский язык,
автор: giannacapriati
Предмет: Русский язык,
автор: tolacnistov53
Предмет: Алгебра,
автор: Saha174174