Question

Решите 5 задание.
Желательно с объяснениями

Answer 1

Определённый интеграл.

Формула Ньютона-Лейбница.

$\displaystyle \boxed{S=\int\limits^a_b (f(x)-g(x))dx }$

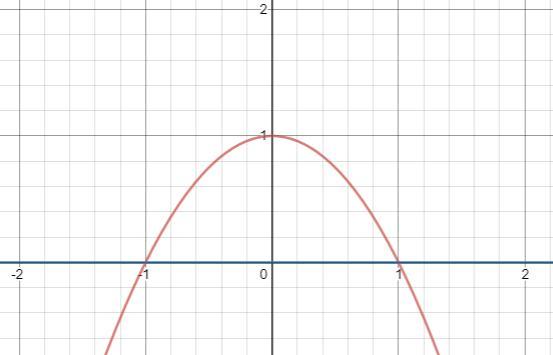
Ф-ции:

$y=1-x^2\;\;\;\;\;y =0$

Построим график функций (смотрите на картинку).

На пересечении графиков найдём верхний и нижний пределы интегрирования.

$a=1\;\;\;\;\;b=-1$

Смотрим на взаимное расположение графиков.

$y=1-x^2$ находится выше, чем $y=0$, поэтому:

$\displaystyle S=\int\limits^1_{-1} {(1-x^2-0)} \, dx = \int\limits^1_{-1} {(1-x^2)} \, dx =\Big(x-\frac{x^3}{3}\Big) \left | {{1} \atop {-1}} \right. =\\\\\\ = (1-\frac{1^3}{3})-(-1-\frac{(-1)^3}{3})=1-\frac{1}{3}+1-\frac{1}{3} =\frac{4}{3}$