Добрый день, очень нужна ваша помошь. Нужно решить задачу на оптимизацию. Есть прямоугольный треугольник ABC (A - прямой угол).
AC = 3, AB = 4, BC = 5, где то на AC есть точка N, где то на AB есть точка M и где то на BC есть точка K. Итак точки M, N, K и прямой угол треугольника образуют прямоугольник внутри треугольника. Мы можем двигать точку K по гипотенузе (BC - гипотенуза) и получать прямоугольники разных площадей. Вопрос! какую максимальную площадь прямоугольника можно получить, двигая таким образом точку, если x в данной задаче это отрезок KC?
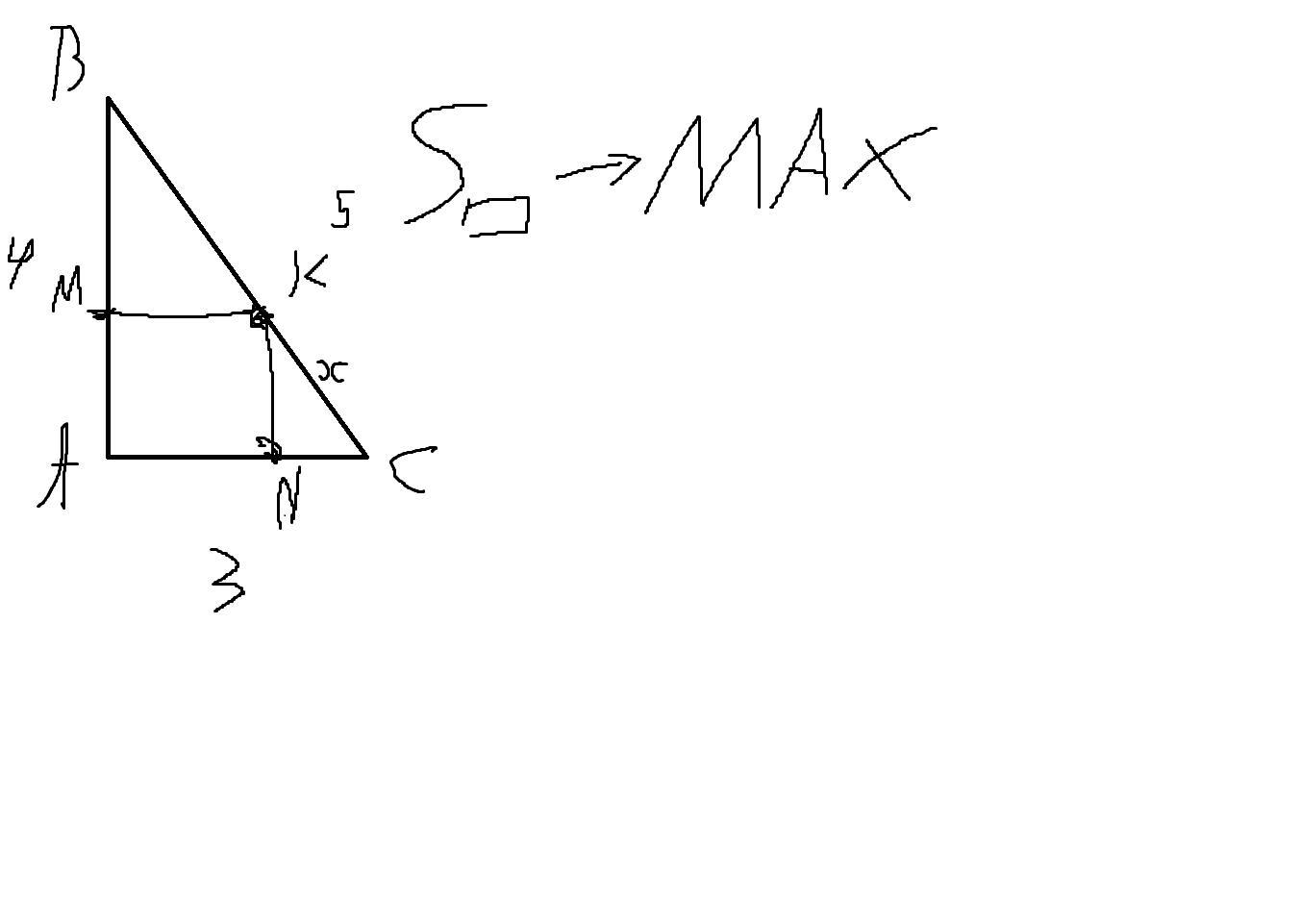
Ответы
Есть прямоугольный треугольник ABC (A - прямой угол).
AC = 3, AB = 4, BC = 5, где то на AC есть точка N, где то на AB есть точка M и где то на BC есть точка K. Итак точки M, N, K и прямой угол треугольника образуют прямоугольник внутри треугольника. Мы можем двигать точку K по гипотенузе (BC - гипотенуза) и получать прямоугольники разных площадей. Вопрос! какую максимальную площадь прямоугольника можно получить, двигая таким образом точку, если x в данной задаче это отрезок KC?
Пошаговое объяснение:
S( прямоуг.)= MK*KN . Площадь должна быть наибольшей. Выразим стороны MK и KN через х.
Пусть КС=х, 0<х<5. Тогда ВК=5-х.
ΔNKC подобен ΔАВС по 2-м углам, значит сходственные стороны пропорциональны KN:АВ=КС:ВС или KN:4=х:5⇒ KN=0,8х.
ΔМВК подобен ΔАВС по 2-м углам, значит сходственные стороны пропорциональны :
МК:АС=ВК:ВС или МК:3=(5-х):5 ⇒ МК=(15-3х):5=3-0,6х.
S( прямоуг.)= 0,8х*(3-0,6х)=2,4х-0,48х² , S'( х)=2,4-0,96х .
S'( х)=0 при х=2,5 ( критическая точка).
S'( х) + -
-----------------------(2,5)-----------------------
S( х) возр max убыв
Т.о. при х=2,5 функция S( х) достигает своего максимального значения .
KN=0,8*2,5=2
МК=3-0,6*2,5=1,5.
S(прямоуг.) =2*1,5=3 (ед²)