Предмет: Алгебра,
автор: alinasytnikova2004
Вычислите интегралы
Приложения:
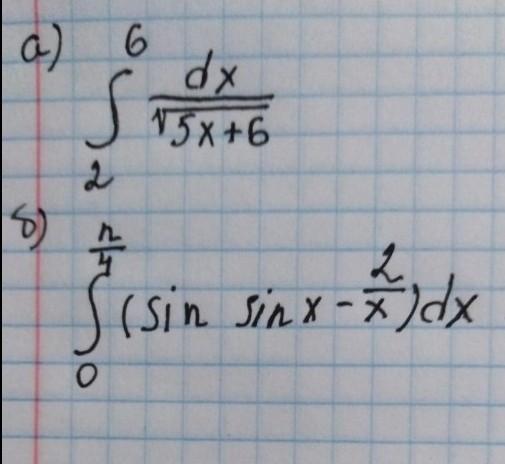
Ответы
Автор ответа:
2
На счёт второго примера я не уверен (по сути, решения нет). Но Вы тоже пересмотрите условие, может не так записали? Или это уже моя ошибка... :
Приложения:

alinasytnikova2004:
Я все правильно записала
Тогда, получается, решения нет (или, как написал другой ответчик, "интеграл не является определённым". Можете теперь с двумя ответами свериться, чтобы быть уверенной окончательно).
Автор ответа:
2
Ответ:
Так как под знаком интеграла присутствует дробь, в знаменателе которой содержится х, то тогда х≠0. Предел же интегрирования содержит число 0. Интеграл не является определённым.
Спасибо за Ваш ответ. Помогли даже мне))
Похожие вопросы
Предмет: Русский язык,
автор: AnHeLiS2003
Предмет: Английский язык,
автор: larisik17121974
Предмет: Русский язык,
автор: плае
Предмет: Литература,
автор: sshachin701
Предмет: Математика,
автор: дшршмд