Question

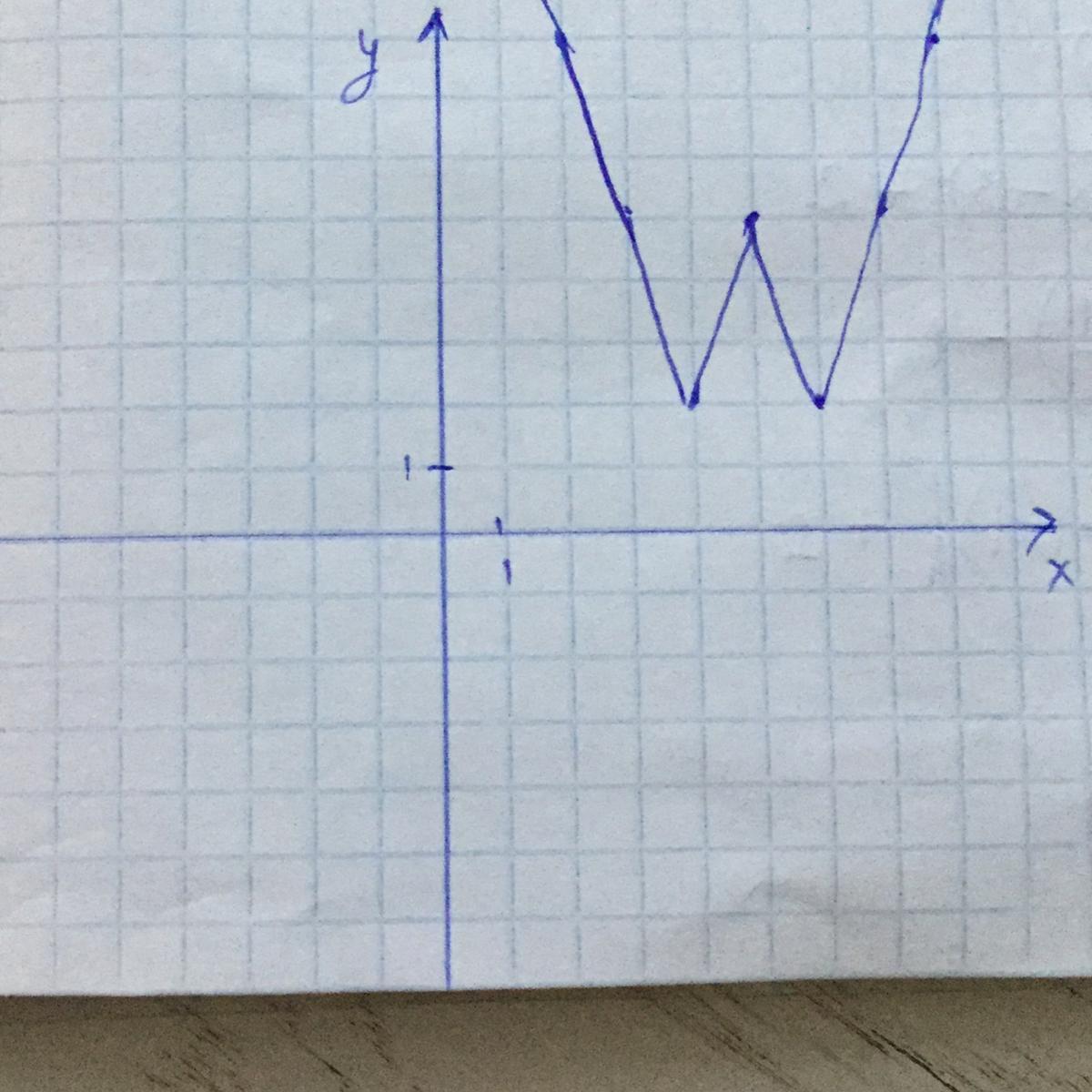
найти формулу к этому графику функций

Answer 1

Ответ: $F(x) = | | -3x+ 15| -3| + 2$

Объяснение:

Попробуем составить функцию с таким графиком. Заметим, что функция имеет форму W, а значит модуль был применен два раза. Заметим, что "уголок" - это часть функции, отраженная относительно OX. Обозначим, нашу показанную функцию как F, на шаге до этого как f1. Тогда:

$F(x) = |f_{1}(x) | + 2$

+2 - так как нижние уголки сдвинуты наверх на 2.

Теперь заметим, что высота уголка направленного вверх равна 3. Значит была некоторая функция f2 от которой взяли модуль опустили на 3 и получили f1. Запишем это:

$F(x) = | |f_{2}(x) | - 3| + 2$

Заметим, что f2 была функцией вида kx+b (примите как факт). Попробуем составить уравнение прямой, которая бы соответствовала рисунку:

$x_{1} = 5 \ \ y_{1} = 0\\k = \frac{delta\ y}{delta\ x} = -3$

k определяем по наклону левой части графика W. Решаем уравнение:

$kx_{1} +b = y_{1}\\-3* 5 + b = 0\\b = 15$

Отсюда получаем функции:

$f_{2} = -3x+15\\F(x) = | | -3x+ 15| -3| + 2$