Предмет: Математика,
автор: Mathlover357
Помогите пожалуйста
Как решать такие примеры
Приложения:
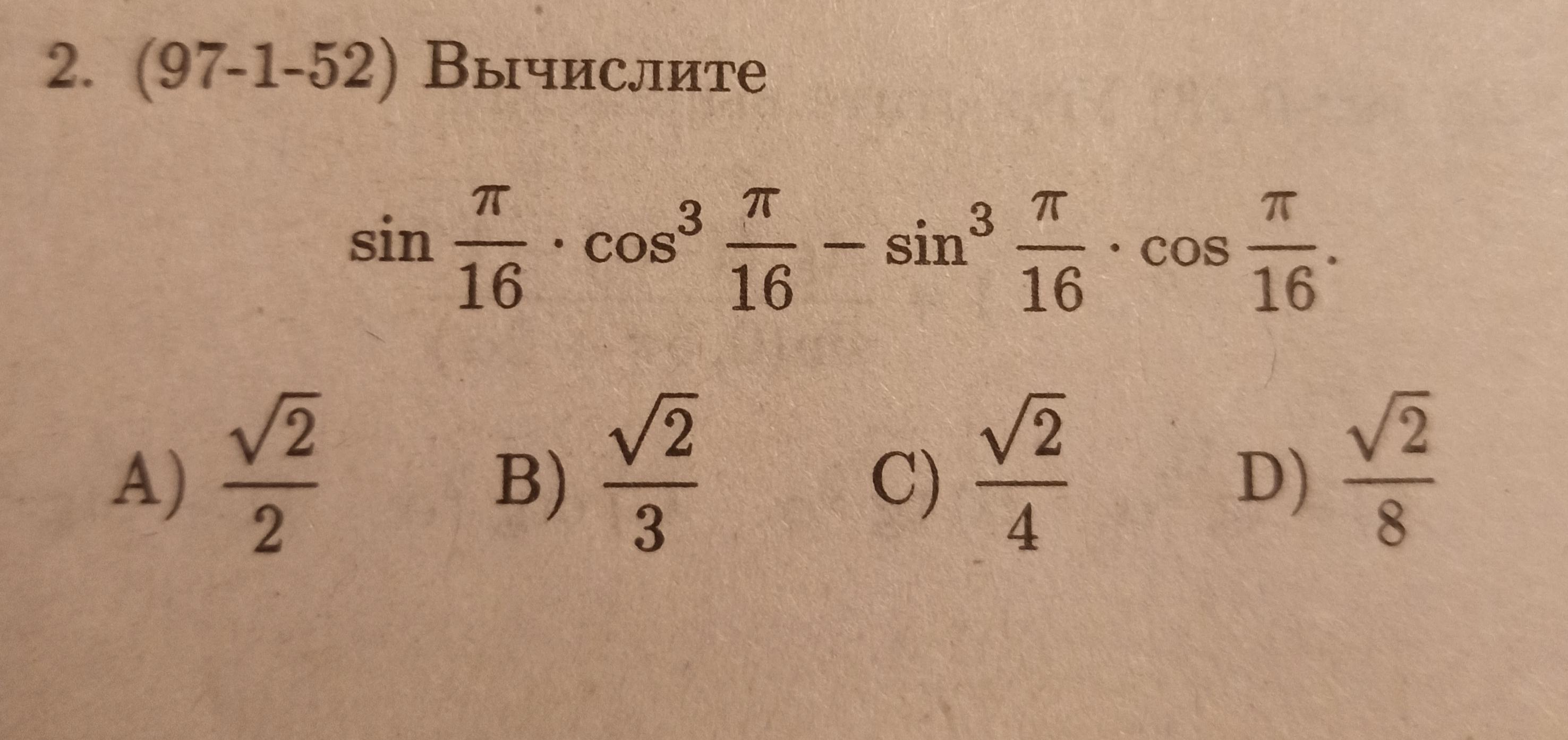
Ответы
Автор ответа:
0
При вычисление использовали формулы синус двойного угла sin2x=2sinxcosx и косинус двойного угла cos2x=(cosx)^2-(sinx)^2
Ответ: D)
Похожие вопросы
Предмет: Русский язык,
автор: dancestar2013
Предмет: Русский язык,
автор: Аноним
Предмет: Українська мова,
автор: 1102004www
Предмет: Алгебра,
автор: ТЁмиик