Предмет: Математика,
автор: Student194
Вычислить производные функции при данном значении аргумента.
Просьба решение написать па листочке
Приложения:
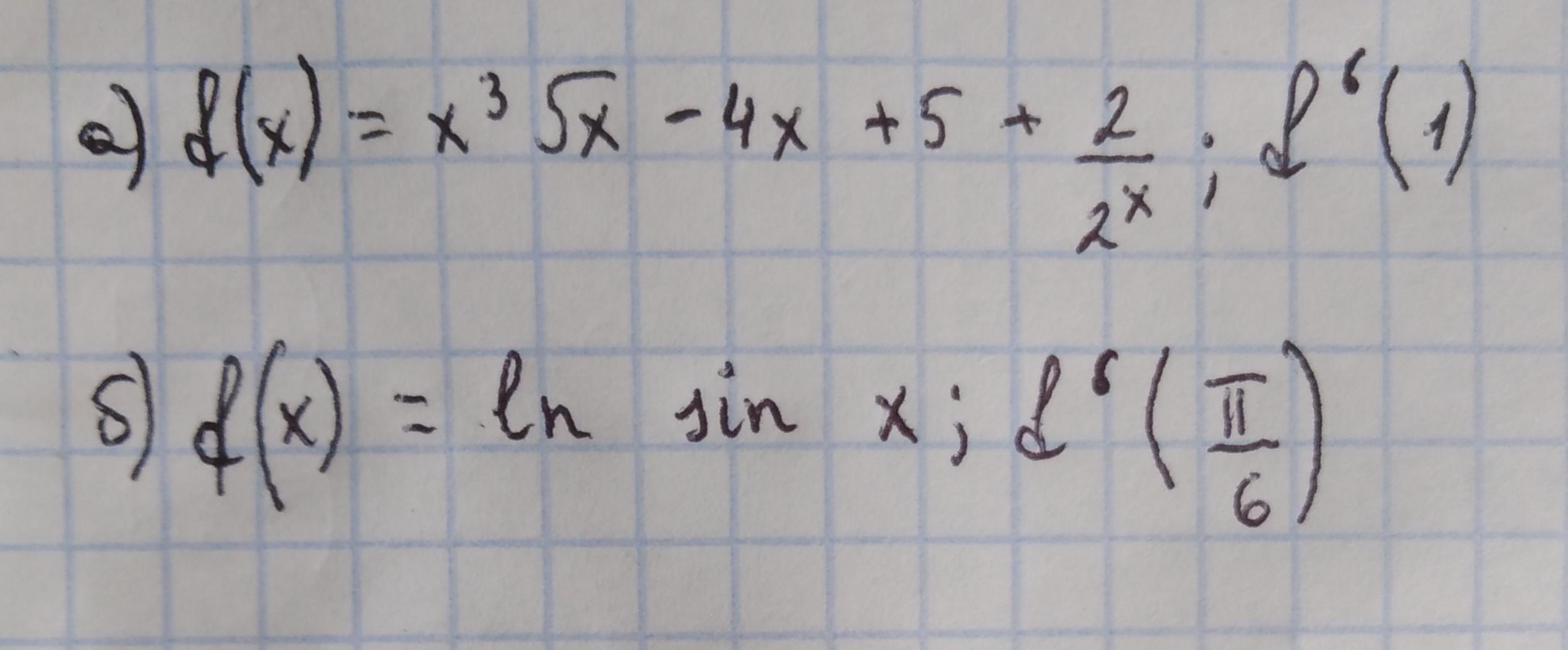
Ответы
Автор ответа:
1
Пошаговое объяснение:
Ответ: 7,5-ln2.
Ответ: √3.
Похожие вопросы
Предмет: Английский язык,
автор: zaqwsx22082000
Предмет: Другие предметы,
автор: 4213
Предмет: Русский язык,
автор: ekaterinakalyu
Предмет: Математика,
автор: kuvanovaleks
Предмет: Литература,
автор: gustovsanek