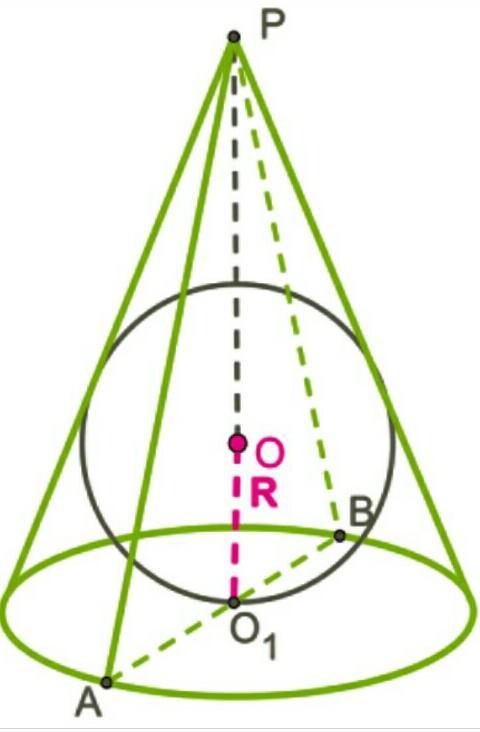
В конус у которого осевое сечение – правильный треугольник вписан шар. Найдите площадь поверхности шара, если образующая конуса равна 3 см.
Ответы
Дано:
Шар вписан в конус.
Осевое сечение конуса - правильный △АВР.
АР = РВ = АВ = 3 см
Найти:
S поверхности шара - ?
Решение:
Так как △АВР - правильный ⇒ он ещё и равнобедренный.
РО₁ - высота.
"Высота, проведённая из вершины равнобедренного треугольника к основанию равнобедренного треугольника, является его медианой и биссектрисой".
⇒ АО₁ = О₁В = 3/2 = 1,5 см, так как РО₁ - медиана.
Найдём высоту РО₁, по теореме Пифагора: (с = √(а² + b²), где с - гипотенуза; а, b - катеты).
а = √(c² - b²) = √(3² - 1,5²) = (3√3)/2 (см).
Итак РО₁ = (3√3)/2 (см).
АО₁ = 1,5 (см).
РО₁ = 3√3/2 (см).
⇒ S△ABP = 1/2 · PO1 · AB = PO1 · AO1 = 1,5 · 3√3/2 = 9√3/4 (см²).
АР = РВ = АВ = 3 (cм).
p - полупериметр.
р = АР + РВ + АВ/2 = 3 + 3 + 3/2 = 4,5 (см).
R вписанного шара (ОО1) = S△ABP/p = 9√3/4 : 4,5 = √3/2 (см).
S поверхности шара = 4пR².
или
S поверхности шара = пD².
D = 2R
S поверхности шара = п(4 · (√3/2)²) = п(3/4 · 4) = 3п см²
S поверхности = п(√3/2 · 2)² = п((√3)²) = 3п см²
Ответ: 3п (см²).