Предмет: Геометрия,
автор: dianagulaja28
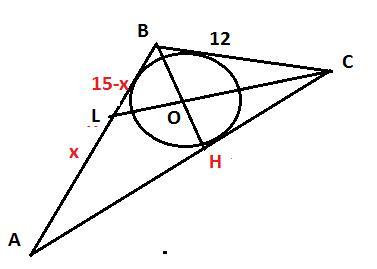
У трикутнику ABC AB=15 см BC=12 см AC=18 см . У якому відношенні центр кола вписаного у трикутник ABC ділить бісектрису трикутника CL.
ужнеужели:
В общем так, смотри на мое решение и это дай твоему учителю.Он это примет. Все остальное от лукавого
Ответы
Автор ответа:
14
Ответ: отношение 2:1
Объяснение: Не мог набрать на клавиатуре.
Приложения:

Блин, Вы знаете школьную программу?
Я учитель
Мне главное, что бы была логика в действиях. Человек, который пользуется готовыми формулами не умеет думать. А когда он дорастет до "думать" ему не нужны костыли готовых формул. Только это очень тяжело. И готовые решения продвинутых пользователей вроде Вас, дают им надежду, что геометрия алгоритмическая наука. Вы - при всей Вашей просвещенности - зло! Надеюсь, не обидел Вас.
Обана! Вот ответ! Тут гений геометрии ниже дал ответ. Проанализируйте, Valenivan, ситуацию. Чему он и Вы научили ученика.В чем смысл нашего сайта - давать решения. Но такие, что бы были поняты ученикам.
Ну вот, слились. А жаль, ведь умеете думать.
Ну вот не пр5едполагал, что такая п
Ну вот не предпогал, что такая прм
Ну вот не предполагал, что такая примитивная задача будет иметь такой резонанс.
Автор ответа:
29
Можно использовать свойство центра вписанной окружности как точки пересечения биссектрис:
Каждая биссектриса треугольника делится точкой пересечения биссектрис в отношении суммы прилежащих сторон к противолежащей, считая от вершины.
В нашем случае (12 + 18) / 15 = 30/15 = 2/1.
Благодарю Вас, Магистр! Спасибо! Вы великолепны!
Вы так много объяснили учащемуся, что я благоговею! СПАСИБО, МАГИСТР!
Блин! Как хорошо, что Вы здесь есть!
Похожие вопросы
Предмет: Русский язык,
автор: Домик3107
Предмет: Русский язык,
автор: Оля190
Предмет: Русский язык,
автор: lizagura
Предмет: История,
автор: 12345kirill12345
Предмет: Математика,
автор: аирао