Предмет: Математика,
автор: sadanimex
Помогите пожалуйста!!!
Приложения:
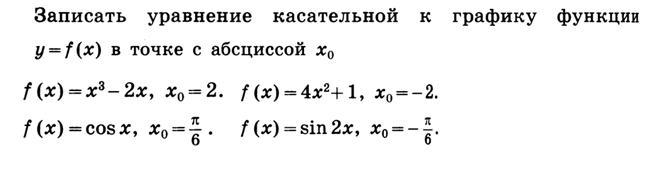
Ответы
Автор ответа:
1
Ответ:
1)
2)
3)
4)
Пошаговое объяснение:
1)
2)
3)
4)
Похожие вопросы
Предмет: Українська мова,
автор: 2003ak2003
Предмет: Русский язык,
автор: monicasimonyan
Предмет: Русский язык,
автор: Аноним
Предмет: Математика,
автор: мария1665