Question

Помогите СРОЧНО!!!
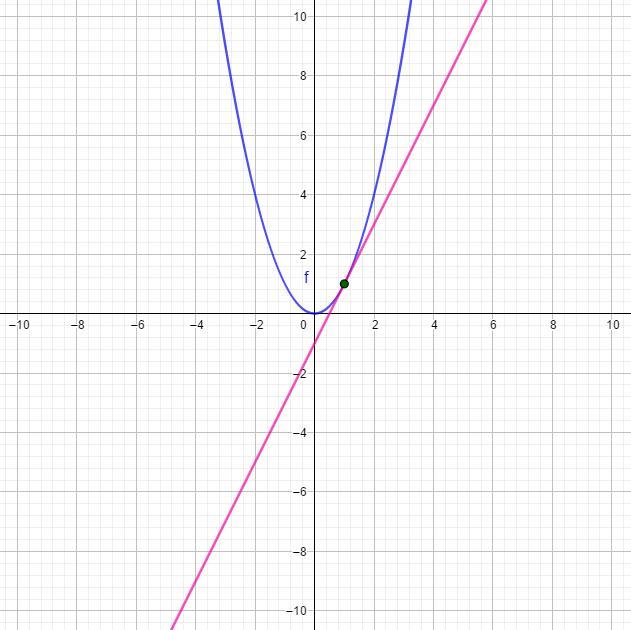
Составьте уравнение касательной к графику функции y=x (в квадрате) в точке A (1;1)

Answer 1

Ответ:     $y=2x-1$.

Решение:

Сначала вспомним уравнение касательной, проходящей через заданную точку:

$\displaystyle y = f \Big (x_0 \Big ) + f'\Big(x_0\Big)\; \Big(x-x_0\Big)$

Что мы знаем? $f \Big (x\Big)=x^2$ и $x_0=1$.

Поэтому вначале найдем производную:

$f' \Big ( x \Big ) = \Big (x^2 \Big)' = 2 \cdot x^{2-1} = 2x$

$f' \Big (x_0 \Big) = f' \Big (1 \Big ) = 2 \cdot 1 = 2$

Далее все подставляем в уравнение касательной:

$y = f\Big(1\Big) + f'\Big(1\Big) \; \Big (x-1 \Big)\\\\y = 1^2 + 2 \; (x-1)\\\\y = 1 + 2x-2\\\\y = 2x-1$

Задача решена, и все, что происходит на плоскости, изображено на картинке ниже: