Предмет: Математика,
автор: slava1236676
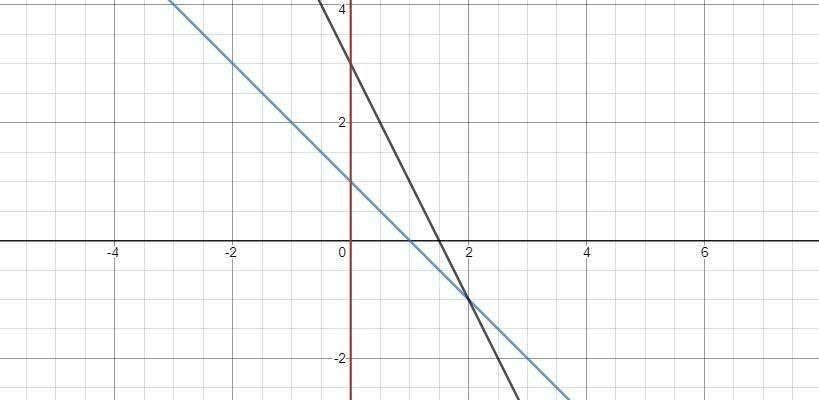
Вычислите с помощью определенного интеграла площадь фигуры, ограниченной линиями: y=1-x, y=3-2x, x=0
Ответы
Автор ответа:
1
Ответ:
2
Пошаговое объяснение:
Находим точку пересечения графиков
Приложения:
Похожие вопросы
Предмет: Русский язык,
автор: tatyanagoldko
Предмет: Русский язык,
автор: smirnovayulia123
Предмет: Русский язык,
автор: bwv605
Предмет: Математика,
автор: MilaAngels4
Предмет: Математика,
автор: EGOR38