Предмет: Математика,
автор: MimiUser
Найти производные следующих функций:(C решение) ПОЖАЛУЙСТАААААА
Приложения:
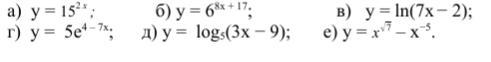
Ответы
Автор ответа:
1
Ответ:
a)
б)
в)
г)
д)
е)
Пошаговое объяснение:
а)
б)
в)
г)
д)
e)
MimiUser:
<3
Похожие вопросы
Предмет: Русский язык,
автор: gnatyukkarina
Предмет: Русский язык,
автор: akbarojan
Предмет: Українська мова,
автор: dasha030807
Предмет: Математика,
автор: Герман6776