Предмет: Геометрия, автор: vodasha06

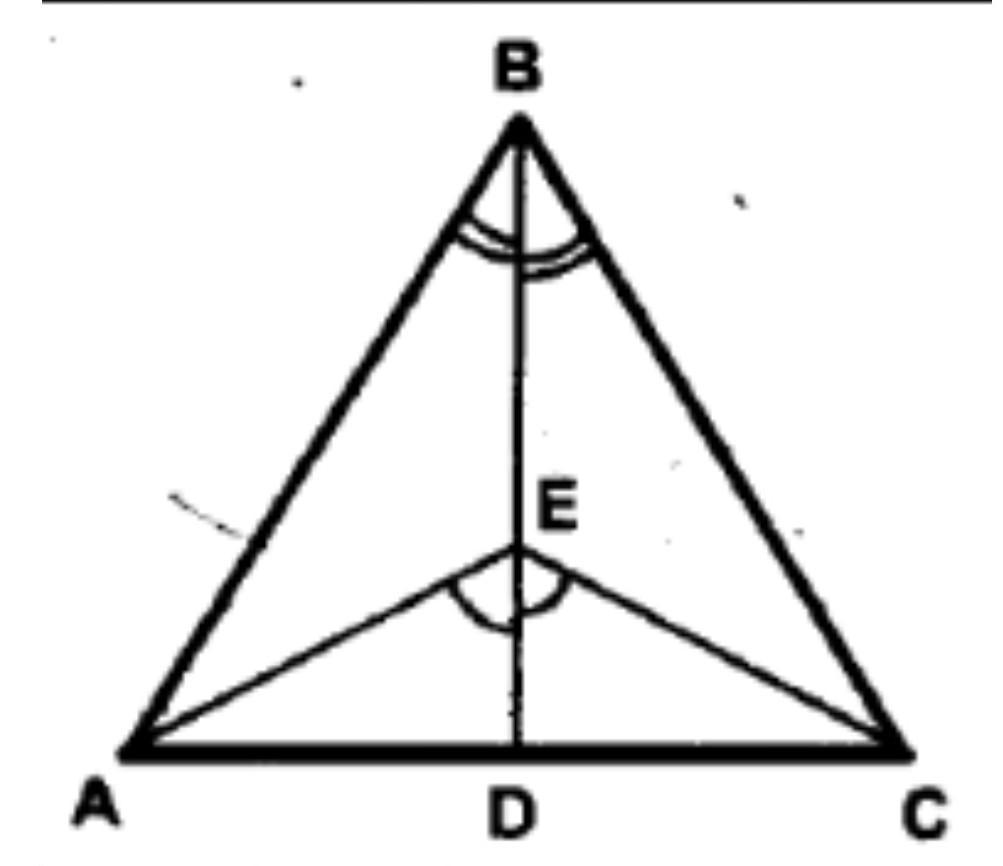
Доказать,что треугольник АВС равнобедренный

Приложения:

yugolovin: В треугольниках AEB и CEB сторона BE общая, углы при вершине B равны по условию, углы при вершине E равны как смежные к равным по условию углам. Поэтому указанные треугольники равны, а тогда AB=CB.

Ответы

Автор ответа: Lizzie2018

Рассмотрим углы AED и CED. Они равны по условию. Следовательно, смежные с ними углы AEB и CEB тоже равны между собой (это следует из теоремы о сумме смежных углов).

Рассмотрим Треугольники АВЕ и СВЕ.

Угол AEB = угол CEB (по выше сказанному), угол АВЕ = угол СВЕ (по условию), а сторона ВЕ - общая. Следовательно, треугольники АВЕ = СВЕ по равной стороне и двум равным прилежащих к ней углам (второй признак равенства треугольников).

В равных треугольниках против равных углов лежат равные стороны. Против угла АЕВ лежит сторона АВ, а против угла СЕВ лежит сторона ВС. Следовательно, АВ = ВС.