Предмет: Алгебра,
автор: СтасДивеев
1)Для функции

найти первообразную, график которой проходит через точку М (-1;2)
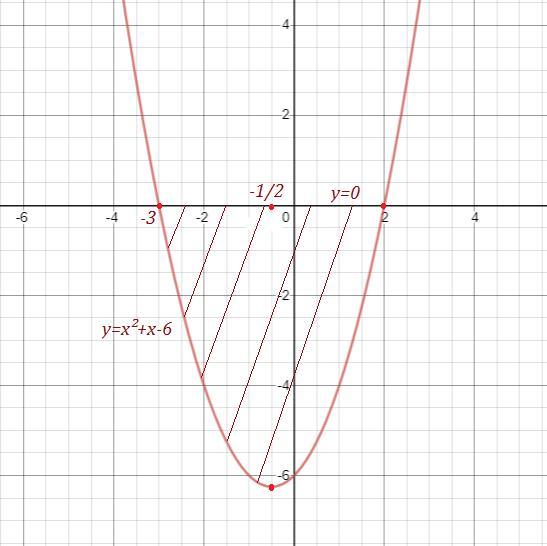
2) Найти площадь фигуры, ограниченной параболой

и прямой осью 0х
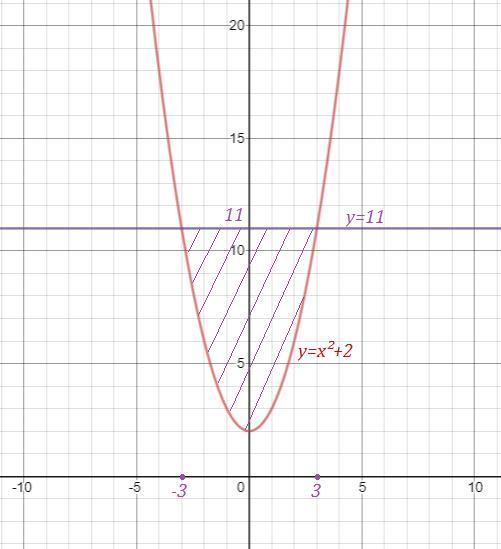
3) Найти площадь фигуры, ограниченной параболой

и прямой

Ответы
Автор ответа:
1
Приложения:
Похожие вопросы
Предмет: Русский язык,
автор: jazzi132
Предмет: Русский язык,
автор: shalito99
Предмет: Русский язык,
автор: sasha33937
Предмет: География,
автор: пупсик101
Предмет: История,
автор: Killiya