Предмет: Математика,
автор: IvAn4o
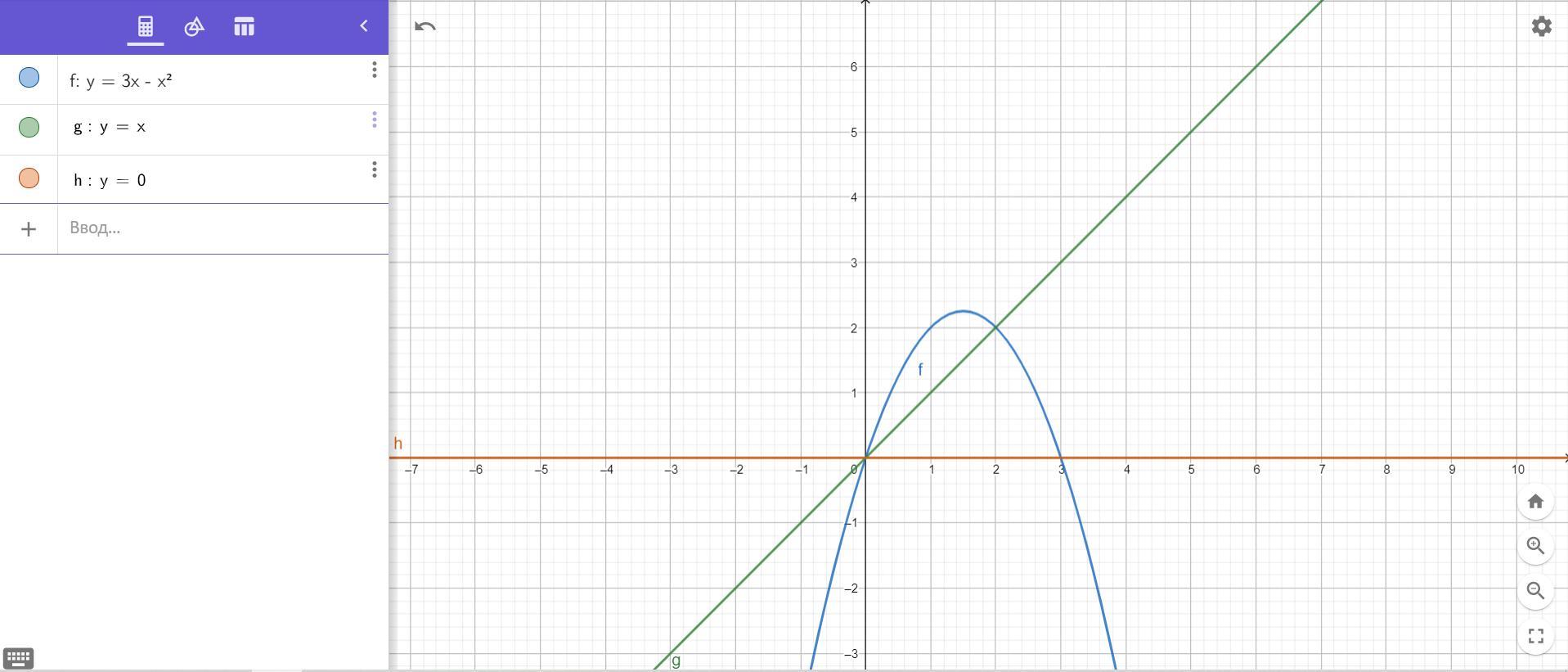
Найти площадь фигуры, ограниченной линиями: y = 3x − x^2
, y = x, и осью Ox
mionkaf1:
"и осью Ох" не лишнее?
Нет не лишнее
тогда понял
Cпасибо вам, вы мой спаситель
Ответы
Автор ответа:
1
См.график
Приложения:
Cпасибо огромнооооооооееее)
Похожие вопросы
Предмет: Английский язык,
автор: bdfynttdrf
Предмет: Русский язык,
автор: Аноним
Предмет: Русский язык,
автор: настяалина
Предмет: Математика,
автор: lisagaga04
Предмет: Математика,
автор: диана2415