Помогите решить координатно-векторным методом, а не геометрическим

Ответы
1)2)-текст на фото.
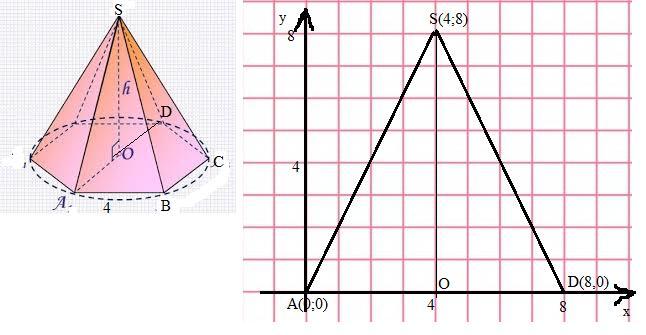
3)Ребро в основании правильной шестиугольной пирамиды SABCDEF равно 4. Высота пирамиды SО равна 8.Найти расстояние от вершины А до середины бокового ребра SD.
Объяснение:
1) Пусть О-точка пересечения диагоналей ромба. По свойству диагоналей ромба О-середина АС .
О( (6+4):2 ; (7+3):2 ;(8+2):2) или О(5;5;5)
2)Вектор ВА (-1;2;0).
Точку D можно получить параллельным переносом на вектор ВА..
Тогда координаты D( 2+(-1) ;0+2;2+0) или D(1;2;2).
3) Основании правильной шестиугольной пирамиды-правильный шестиугольник ABCDEF ; а₆=R=4 , значит AD=8.
Пусть Н середина SD. Введем прямоугольную систему координат с началом в точке А и осью ох, совпадающей со стороной АD .Найдем координаты точек :А(0;0) , D(8;0) , S(4;8) .
Тогда координаты середины Н (6;4).
АН=√( (6-0)²+(4-0)²)=√52=4√13.