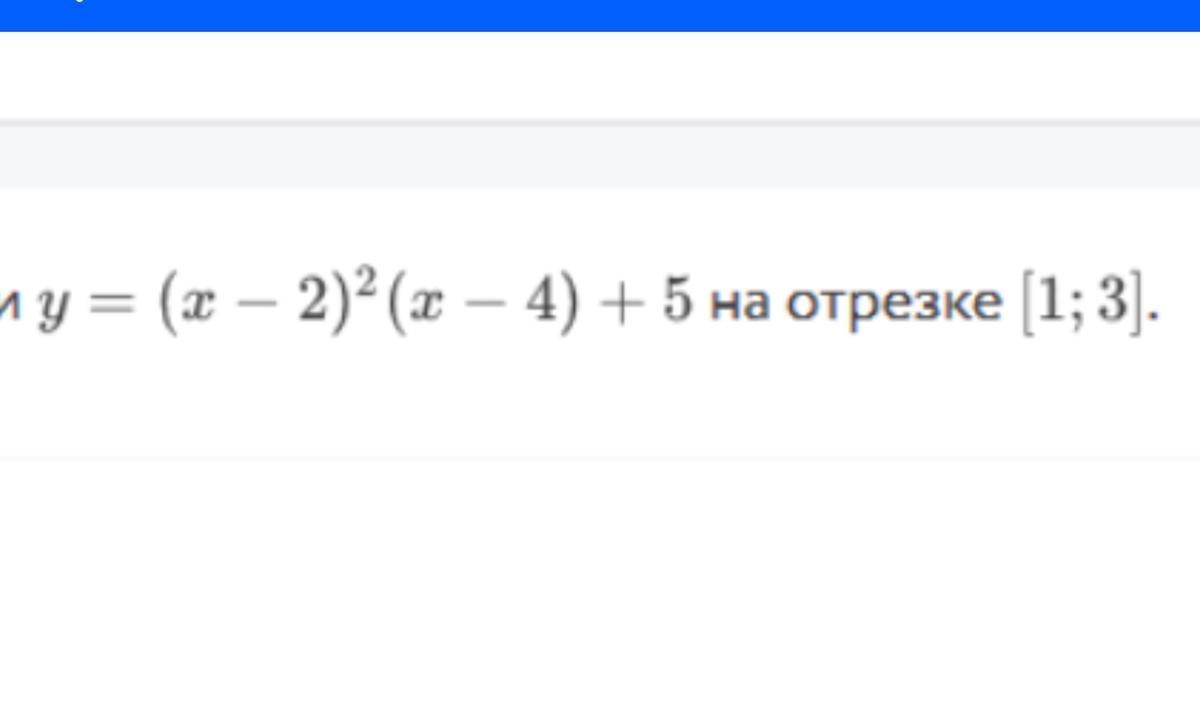
Найдите наибольшее значение функции (на фото)
На отрезке [1;3]
Ответы
Ответ:
f наиб = 5; f наим = 2
Пошаговое объяснение:
Функция
у = (х - 2)²(х - 4) + 5
Производная функции
у' = 2(x - 2)(x - 4) + (x - 2)²
у' = 2(x² - 6x + 8) + x² - 4x + 4
у' = 2x² - 12x + 16 + x² - 4x + 4
y' = 3x² - 16x + 20
Найдём точки экстремумов
3x² - 16x + 20 = 0
D = 256 - 240 = 16 = 4²
x₁ = (16 - 4)/6 = 2 (точка максимума)
х₂ = (16 + 4)/6 = 10/3 = 3 1/3 (точка минимума)
Поскольку точка максимума находится внутри интервала [1; 3], то наибольшее значение функция принимает в этой точке
f наиб = f max = f(2) = (2 - 2)² (2 - 4) + 5 = 5
Для определения наименьшего значения функции найдём её значения на концах интервала
f(1) = (1 - 2)² (1 - 4) + 5 = 2
f(3) = (3 - 2)² (3 - 4) + 5 = 4
Наименьшее значение функция имеет на левой границе интервала, при х = 1 f наим = f(1) = 2