Предмет: Геометрия, автор: lisergin

помогите решить пожалуйстаааа

Приложения:

Ответы

Автор ответа: Iife20

Ответ:

Объяснение: ЗАДАНИЕ 1А)

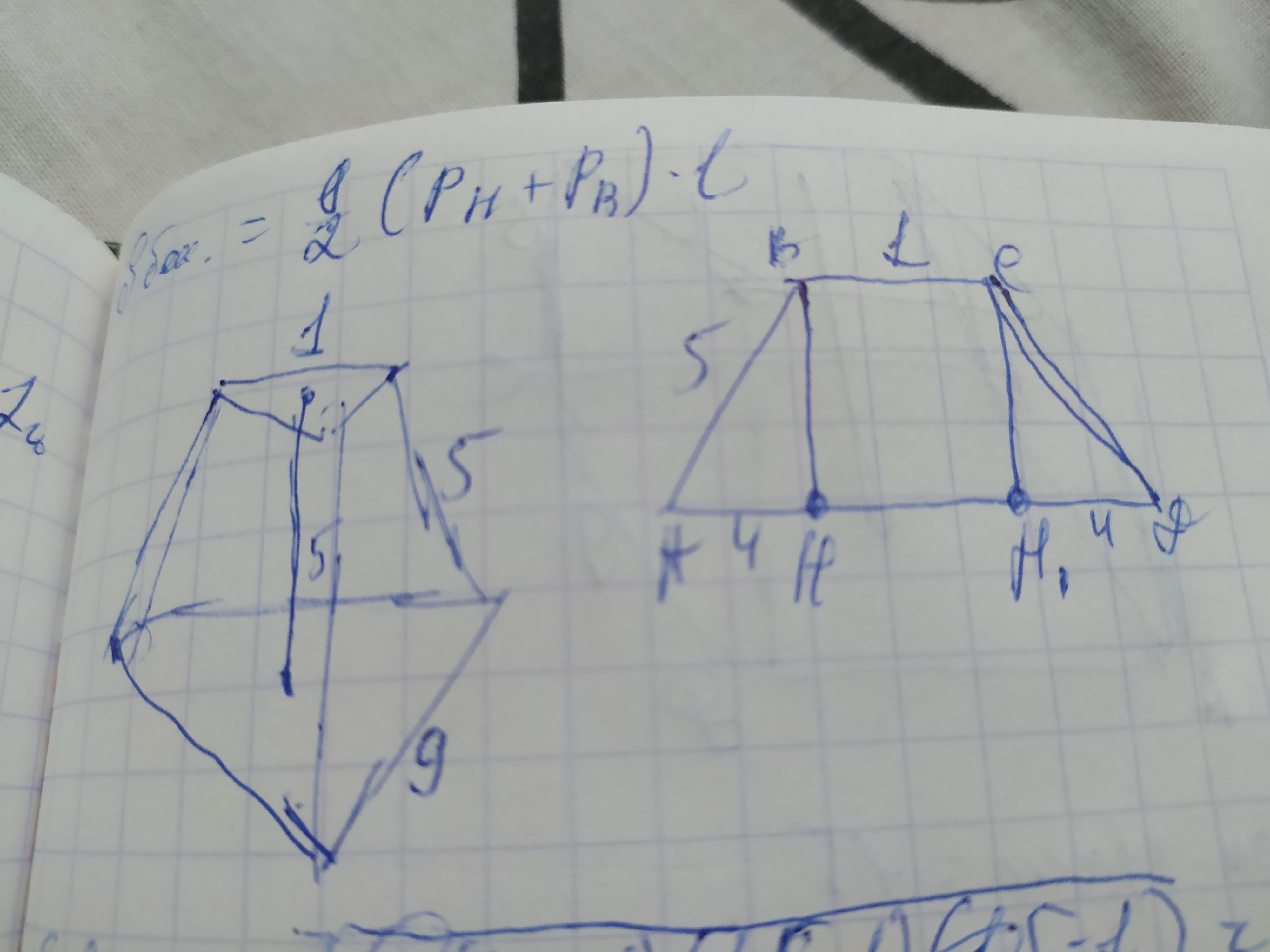
Найдём апофему. Так как боковой гранью усечённой пирамиды является трапеция, то мы сможем вычислить её апофему, т.е. высоту трапеции. Обозначим вершины трапеции А В С Д, с основанием ВС=1см и АД =9см и боковыми сторонами АВ и СД, причём АВ=СД=5см. Проведём к нижнему основанию АД две высоты ВН и СН1. Они делят сторону АД так что НН1=ВС=1см. Остальные отрезки трапеции АН +ДН1 составляют в сумме: 9-1=8см. Так как трапеция равнобедренная то:

АН=ДН1=8÷2=4см.

У нас получился прямоугольный треугольник АВН с катетами АН и ВН и гипотенузой АВ. Найдём по теореме Пифагора ВН:

ВН²=АВ²-АН²=5²-4²=25-16=9; ВН=√9=3см

ОТВЕТ: а) апофема ВН=3см

ЗАДАНИЕ 1 Б)

Теперь найдём площадь боковой грани, т.е. площадь трапеции по формуле:

S=(BC+АД)/2×ВН=

=(1+9)/2×3=10/2×3=5×3=15см²

ОТВЕТ: б) Sбок.грани=15см²

ЗАДАНИЕ 1В)

Зная площадь боковой грани, найдём площадь боковой поверхности пирамиды. Так как таких граней в пирамиде 3, то:

Sбок.пов=15×3=45см²

ОТВЕТ: в) Sбок.пов=45см²

ЗАДАНИЕ 1 Г)

Так как основаниями правильной 3-угольной усечённой пирамиды являются равносторонние треугольники, найдём площадь верхнего основания по формуле площади равностороннего треугольника: S=a²√3/4, где а- сторона основы: Sв.осн=1²×√3/4=1√3/4=√3/4см²=

=0,25√3см²

ОТВЕТ: г) Sв.осн=0,25√3см²

ЗАДАНИЕ 1Д)

По этой же формуле найдём площадь нижнего основания пирамиды:

Sниж.осн=a²√3/4=9²√3/4=81√3/4=

=20,25√3см²

ОТВЕТ: Д) Sниж.осн=20,25см²

ЗАДАНИЕ 1Е)

Теперь найдём полную площадь боковой поверхности, для этого сложим сумму площадей двух оснований с боковой площадью пирамиды:

Sпол=Sбок.пов+ Sдвух.осн:

=45+0,25√3+25,25√3=45+20,5√3=

=65,5√3см²

ОТВЕТ: е) Sпол=65,5см²

ЗАДАНИЕ 2

Здесь уже не понадобится искать апофему и площадь трапеции, поскольку мы нашли их в первом задании, но их используем, поскольку высота и площадь трапеции не поменяются. Начнём с ЗАДАНИЯ 2В)

Поскольку основаниями в четырёхугольной пирамиде являются квадраты, то площадь боковой грани умножается на 4 и мы можем найти площадь боковой поверхности усечённой пирамиды:

Sбок.пов=15×4=60см²

ОТВЕТ: Sбок.пов=60см²

ЗАДАНИЕ 2 Г)

Найдём Sвер.осн. по формуле S= а²,

Sвер.осн=1²=1см²

ОТВЕТ: Sвер.осн=1см²

ЗАДАНИЕ 2 Д)

Точно так же найдём площадь нижнего основания: Sниж.осн=9²=81см²

ОТВЕТ: Sниж.осн=81см²

ЗАДАНИЕ 2 Е)

Теперь найдём полную площадь поверхности:

Sпол=Sдвух.осн+Sбок.пов