Предмет: Алгебра,
автор: nesteanastya56
Вычислить определенный интеграл
Приложения:
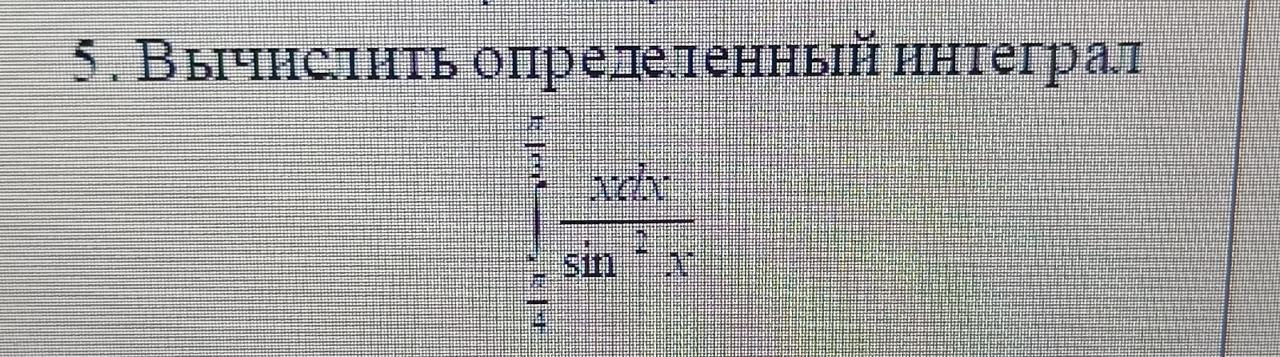
Ответы
Автор ответа:
0
Похожие вопросы
Предмет: Русский язык,
автор: drktex
Предмет: Русский язык,
автор: annachess212
Предмет: Русский язык,
автор: milastarostina
Предмет: Математика,
автор: egorkaboy2005
Предмет: Математика,
автор: gevorjan79