Предмет: Математика,
автор: Ney4Fox
Помогите пожалуйста! Буду очень благодарен! С:

Ответы
Автор ответа:
1
Ответ:
Пошаговое объяснение:
(3n-1)/(3n+2)=(1-1/(3n))/(1+2/(3n))
1/(1+2/(3n))=1-2/(3n)+... (оставляем только n в первой степени)
Тогда
(1-1/(3n))/(1+2/(3n))=(1-1/(3n))*(1-2/(3n)+...)=1-1/n+... (оставляем только n в первой степени)
lim (1-1/n)^4n=exp(-4), так как lim (1-1/n)^n=exp(-1)
Проверяем найденный предел в Maxima
Приложения:
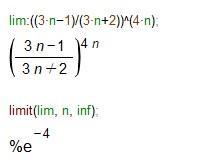
Похожие вопросы
Предмет: Английский язык,
автор: kotelok1
Предмет: Русский язык,
автор: aleksandrovna52
Предмет: Русский язык,
автор: 909811
Предмет: Математика,
автор: minicotikk
Предмет: Химия,
автор: angelina1918