1). Образующая конуса равна 25 см., а радиус основания равен 7 см.
Найдите объём конуса.
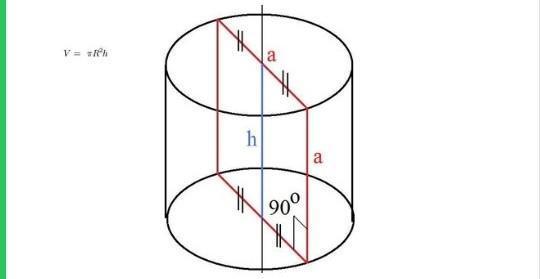
2). Осевое сечение цилиндра является квадрат, площадь которого
равна 36 см2. Найдите площадь основания и объём цилиндра.
Ответы
Ответ:
#1)объем конуса вычисляется по формуле:
V = 1/3 * π* R^2* H
где π=3,14
радиус известен
Найдем высоту, или катет прямоугольного треугольника
образующая - это гипотенуза
радиус будет одним из известных катетов
a= √ (c^2 - b^2)
a= √(25^2 - 7^2)=√ 625 - 49 = √576= 24
V= 1/3 * 3.14 * 49 * 24 = 1231 см^3
#2)Дано:
Осевое сечение цилиндра есть квадрат, площадь которого равняется 36 см. Найти объём цилиндра.
Решение:
Объём прямого кругового цилиндра равен:
V = π * r^2 * h
(где r — радиус основания, h — высота, π ~ 3.14).
Примем диаметр цилиндра за В. Из рисунка и условий задачи ясно, что В = а.
Из рисунка и условий задачи следует, что высота цилиндра h = a
Из условий задачи – осевое сечение цилиндра есть квадрат, площадь которого равняется 36 см.
Отсюда, сторона квадрата равна квадратному корню из 36 (так как площадь квадрата равна квадрату его стороны) – отсюда, сторона квадрата равна 6 см.
Следовательно, диаметр цилиндра В = а = 6 см, его радиус r = а / 2 = 6 / 2 = 3 см
Высота цилиндра h = а = 6 см.
Отсюда, по формуле объёма цилиндра:
V = 3,14 * 3^2 * 6 = 3,14 * 9 * 6 = 169,56
Объём цилиндра равен 169,56 куб. см,