неопределенный интеграл 1+2x/x^2-6x+8 dx
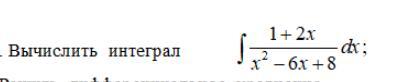
Ответы
Ответ:4,5ln|x-4| -2,5 ln|x-2|+C
Объяснение: Для решения интеграла используем метод неопределённых коэффициентов, для этого разложим знаменатель подинтегральной функции на множители: х²-6х+8=0 ⇒ D=36-32=4 ⇒ х₁=4, х₂=2. Тогда х²-6х+8= (х-4)(х-2)
Получаем разложение знаменателя на множители в подынтегральном выражении: (2х+1)/(х²-6х+8)=(2х+1)/(х-4)(х-2)= А/(х-4) + В/(х-2)= (А(х-2)+В(х-4))/(х-2)(х-4)=(Ах-2А+Вх-4В)/(х-2)(х-4)= ((А+В)х+(-2А - 4В))/(х-2)(х-4) В обеих частях равенства отыскиваем слагаемые с одинаковыми степенями икса и составляем из них систему уравнений: А+В=2 и-2А-4В=1, откуда А=4,5 ; В= -2,5. Значит мы получили следуещее разложение подинтегральной функции:
∫(2х+1)dx/(х²-6х+8)=∫(2х+1)dx/(х-4)(х-2)= ∫4,5dx/(x-4) -∫2,5dx/(x-2)= 4,5ln|x-4| -2,5 ln|x-2|+C
Zadanie 1(Задаание 1).
Найдите деревья со след...
https://znanija.com/task/37686302?utm_source=android&utm_medium=share&utm_campaign=question