Предмет: Математика,
автор: Lalalayka
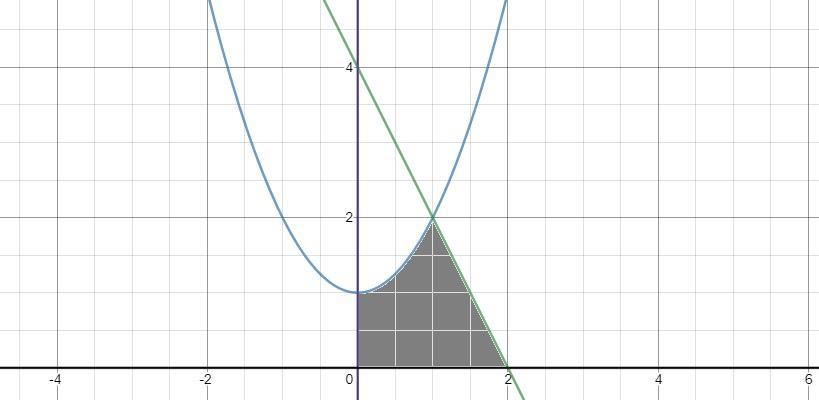
Обчислити площу фігури, обмеженої лініями:

Ответы
Автор ответа:
1
Ответ:
Пошаговое объяснение:
Приложения:
Похожие вопросы
Предмет: Другие предметы,
автор: olesiaivanov2011
Предмет: Русский язык,
автор: MioNastya
Предмет: Русский язык,
автор: artem654321
Предмет: Математика,
автор: Даша3457
Предмет: Литература,
автор: Sveta01042004