Предмет: Алгебра,
автор: zubnojfej
Решите неравенство
Приложения:
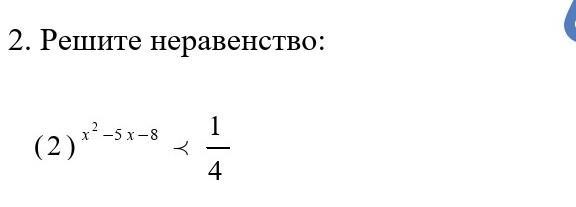
Ответы
Автор ответа:
1
Ответ:
(-1;6)
Объяснение:
для решения показательных неравенств необходимо представить обе части неравенства с одинаковым основанием, тогда:
2^(х^2-5х-8) < 2^(-2)
"отбросим" основания:
х^2-5х-8 < -2
х^2-5х-6 < 0
разложим левую часть на множители, получим:
(х-6)(х+1) < 0
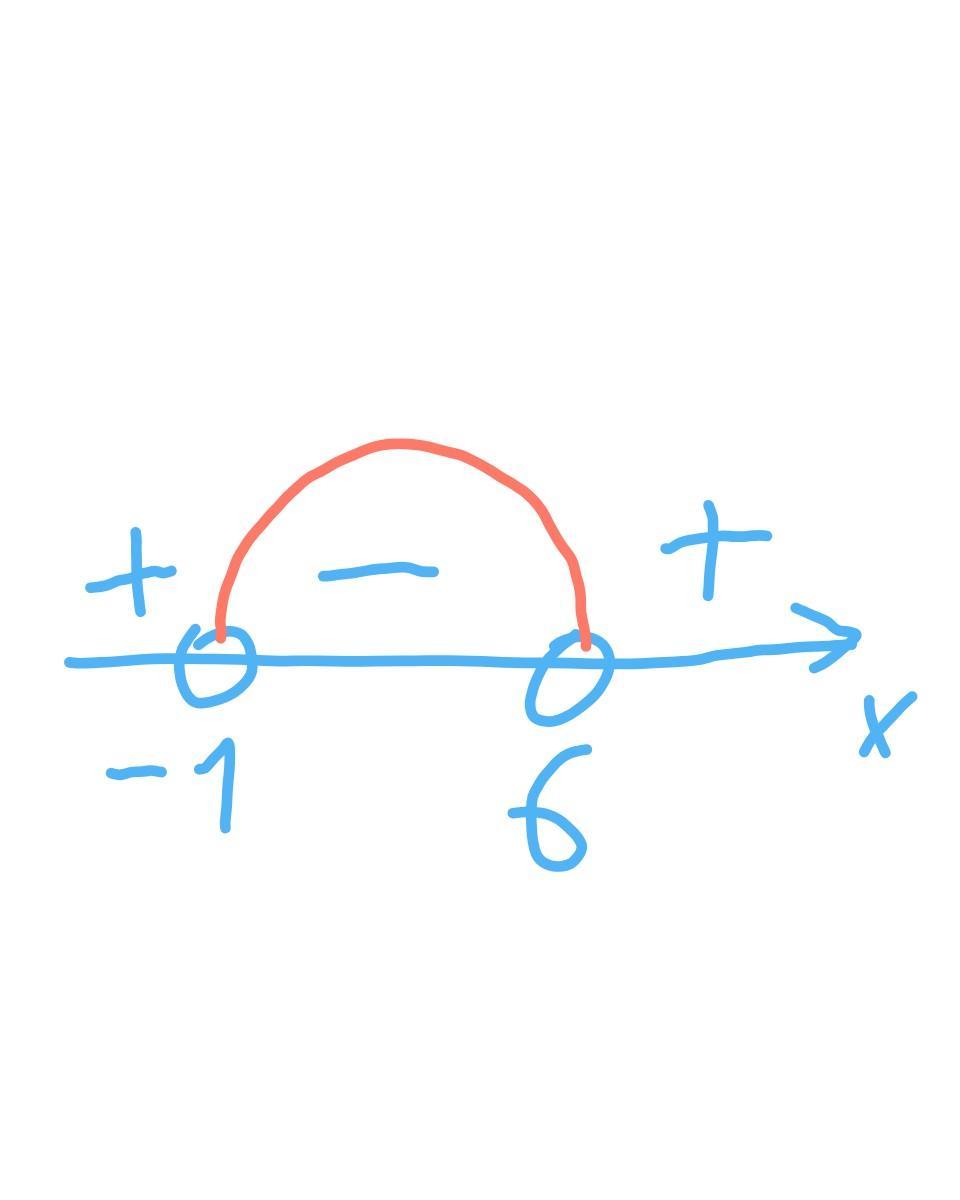
методом интервалов найдем решение(на рисунке). так как неравенство строгое, то точки выколотые, тогда:
х принадлежит (-1;6)
Приложения:
Автор ответа:
1
Объяснение:
-∞__+__-1__-__6__+__+∞
x∈(-1;6).
Ответ: x∈(-1;6).
Похожие вопросы
Предмет: Русский язык,
автор: natalyakorabelskaya
Предмет: Українська мова,
автор: asyasea
Предмет: Русский язык,
автор: 1qaz2wsxs
Предмет: Физика,
автор: pinkjoys
Предмет: Математика,
автор: кролик80