Question

Срочно!!! 40 баллов, можно без решения.
Высота правильной треугольной пирамиды равна 20 см, а угол, который образует апофема с плоскостью основания пирамиды, равен 30°. Вычисли объём пирамиды.

Answer 1

Ответ:

Пошаговое объяснение:

V = 1/3 hSосн

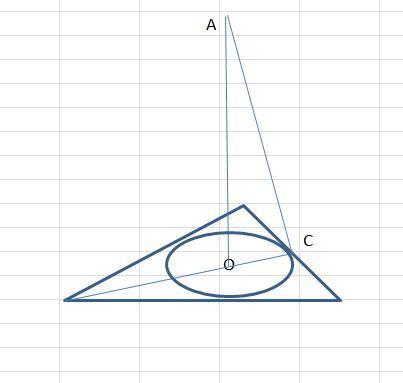
поскольку в основании лежит правильный треугольник, то т.О - центр треугольника и центр вписанной окружности. площадь правильного треугольника через радиус вписанной окружности

$S_{oc} = 3\sqrt{3} *r^{2}$

r = OC

из ΔАОС :

 $OC = h*ctg30 =20\sqrt{3}$

$S_{oc} = 3\sqrt{3} *(20\sqrt{3} )^{2} = 9*400\sqrt{3} = 3600\sqrt{3}$

$V = \frac{1}{3} *20*3600\sqrt{3} = 24000\sqrt{2} (cm^{3})$