Предмет: Математика,
автор: amaliyarahmanina
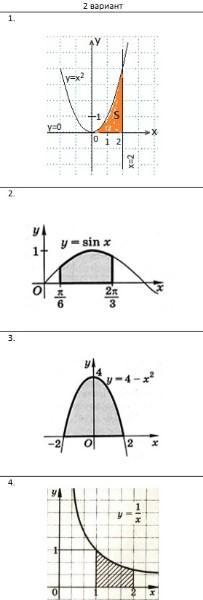
помогите найти площадь криволинейной трапеции, изображенной на рисунке
Приложения:
Ответы
Автор ответа:
3
Ответ:==========
Пошаговое объяснение ВО ВЛОЖЕНИИ
Приложения:
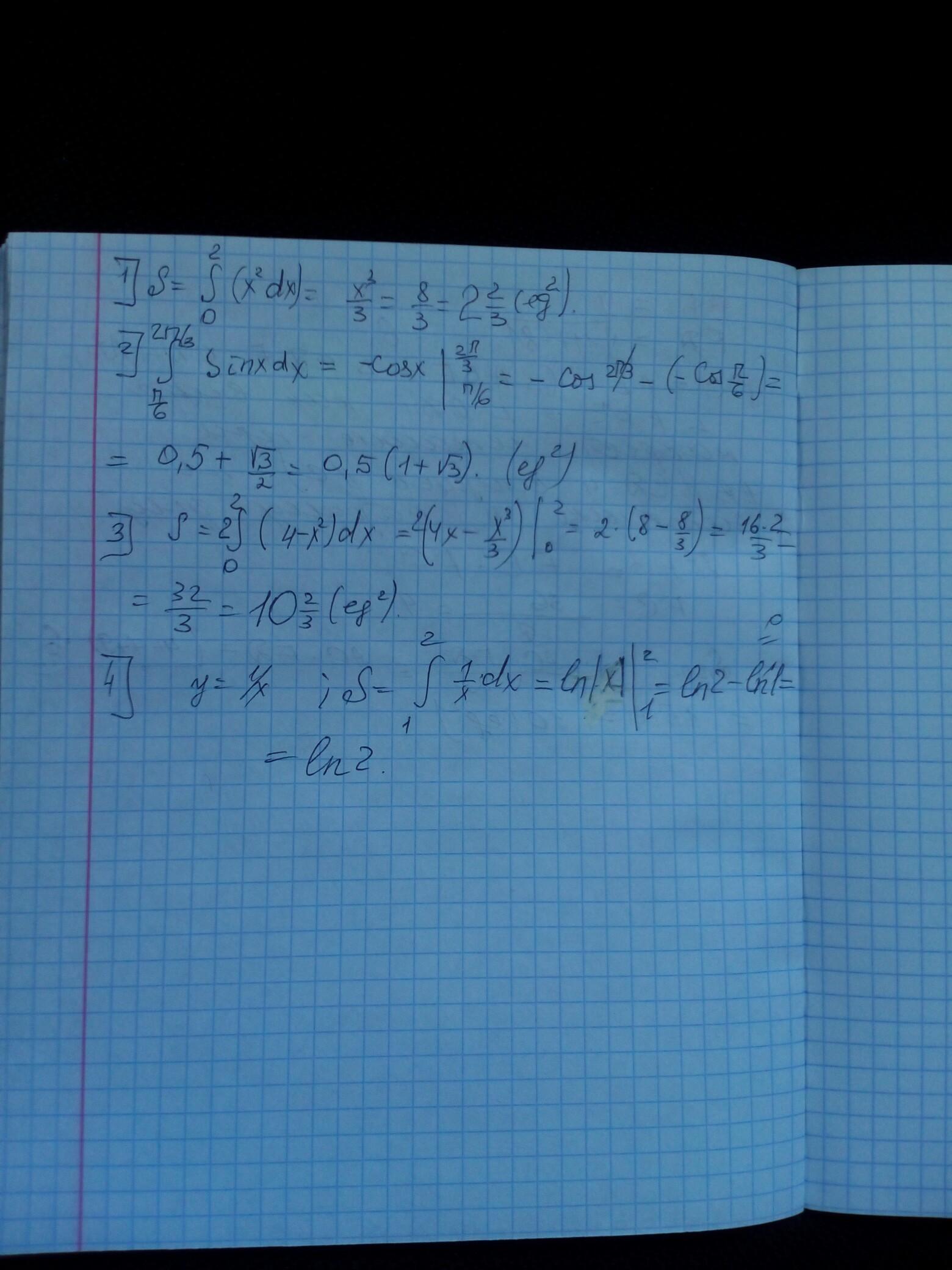
Автор ответа:
2
Похожие вопросы
Предмет: Русский язык,
автор: elina20027
Предмет: Українська мова,
автор: bobuh1972
Предмет: Русский язык,
автор: 89894544584
Предмет: Математика,
автор: casa4
Предмет: Алгебра,
автор: таня647