Предмет: Математика,
автор: newiphone0002
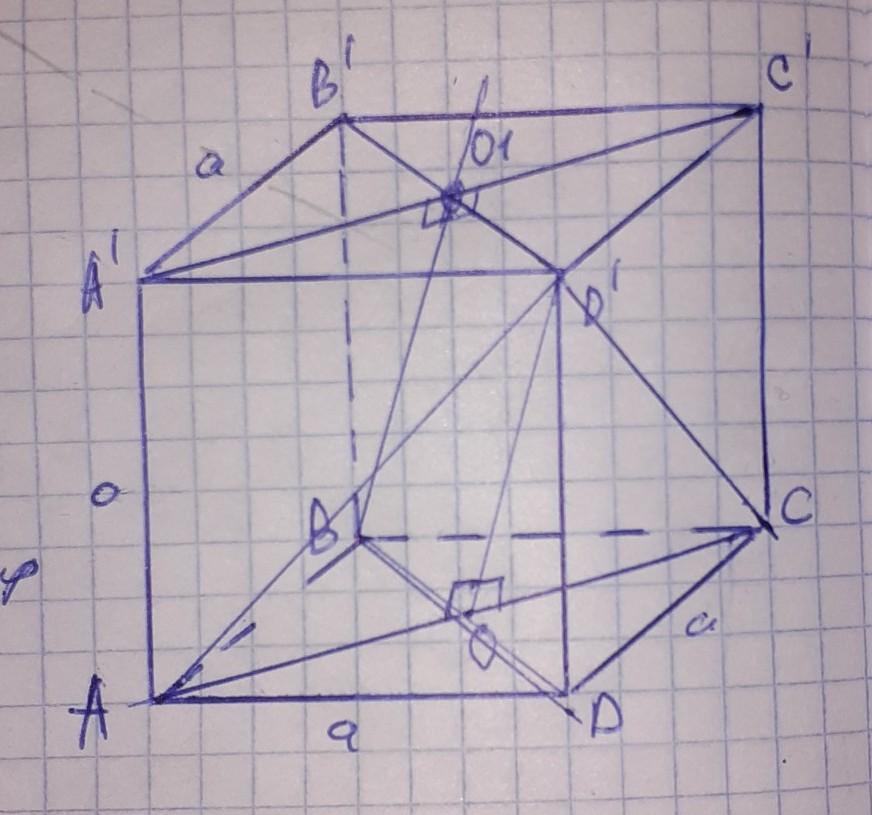
Қырының ұзындығы a - ға тең ABCDA1B1C1D1 кубы берілген. ABCD жағының АС диагоналы арқылы BO1 түзуіне, мұндағы O1 - A1B1C1D1 жағының ортасы, паралллель жазықтық жүргізілген. Қима ауданын табыңыздар.
Ответы
Автор ответа:
12
Пошаговое объяснение:
қима кубтың A C D1 төбелері арқылы өтеді.
кубтың әр жағы квадрат болғандықтан
квадраттың диагоналі d=a√2 тең.
Пифагордың теоремасымен есептегенде
AC=√a²+a²=√2a²=a√2
диагональ жартысы d/2=a√2 /2
АС, AD1 және CD1 диагональдар AC=AD1=CD1=a√2
Тең қабырғалы үшбұрышты ΔАСD1 құрайды.
Пифагор теоремасы бойынша Δ ACD1
биіктігі D1O=√AD1²-AO²=√(a√2)²-(a√2 /2)²=√2a²-2a²/4=√2a²-a²/2=
=√(4a²-a²)/2=√3a²/2=a√3/2
Δ ACD1 ауданы табаны AC=a√2 мен биіктігі D1O=a√3/2 көбейтіндісінің жартысына тең.
S Δ=1/2 × а×h= 1/2×AC× D1O=1/2 ×a√2 ×a√3/2 =
=1/2×a²×√6/2=1/2×a²×√3=(a²√3) /2
тең қабырғалы үшбұрыштың формуласы бойынша
SΔт.қ = а²× (√3 )/4
а қабырға ұзындығы а =AC=AD1=CD1=а√2
SΔт.қ=(а√2)² ×(√3)/4=2×а² ×(√3)/4=(а²√3) /2
Приложения:
Похожие вопросы
Предмет: Русский язык,
автор: SPARTAK2005
Предмет: Українська література,
автор: gaponova98
Предмет: Русский язык,
автор: ЦветковаКатя
Предмет: История,
автор: 005861449
Предмет: Физика,
автор: Liamil130684