Предмет: Геометрия,
автор: krasilnikovad30
Помогите решить подробно задачу.
Центром окружности служит вершина прямого угла С треугольника АВС, радиусом – катет ВС, А=40 градусов. Окружность пересекает стороны АВ и АС с точках D и Е. Определить величину одной из дуг BD или DE.
Ответы
Автор ответа:
1
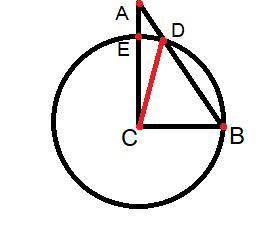
Я сделала чертёж, смотри внизу.
ΔАВС прямоугольный, угол В = 90°-40°=50° (св-во прямоуг.тр.).
Проведём отрезок СD. CD - радиус окружности, как и ВС. Следовательно, ΔСВD равнобедренный, угол СDB=DBC=50°.
Угол DCB=180-(50+50)=180-100=80°.
Угол DCB - центральный угол. Он равен градусной мере ∩DB. Значит, ∩DB=80°.
Я найду и ∩DE. ∩BE=90°, т.к. угол АСВ=90°. Следовательно, ∩ED=90°-80°=10°.
Ответ: дуги BD и DE равны 80° и 10° соответственно.
Приложения:
Похожие вопросы
Предмет: Русский язык,
автор: lerohka02
Предмет: Английский язык,
автор: bicadzeelya
Предмет: Другие предметы,
автор: minionsavik3985
Предмет: Алгебра,
автор: одо1
Предмет: Алгебра,
автор: Kabdulgalieva00