Предмет: Алгебра,
автор: mrkrajson
Вычислить............
Приложения:
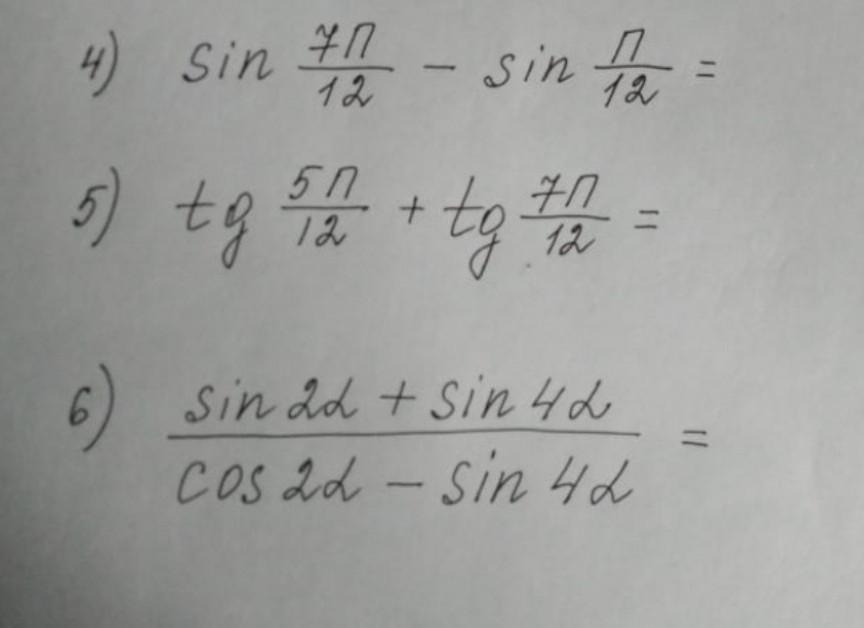
Ответы
Автор ответа:
0
Ответ:
Объяснение:
4) Воспользуемся формулой:
5) Применим формулу:
Похожие вопросы
Предмет: Английский язык,
автор: eldar200
Предмет: Русский язык,
автор: ooleg2024
Предмет: Русский язык,
автор: tru2011
Предмет: Математика,
автор: mahi2005
Предмет: Алгебра,
автор: Jeksenhoran