Предмет: Алгебра,
автор: zyh97498
Найти производную функций ( смотреть скриншот )
Приложения:
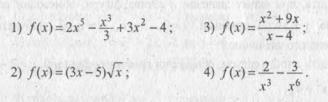
Ответы
Автор ответа:
2
Ответ:
=================================
Объяснение:
Похожие вопросы
Предмет: Русский язык,
автор: efis
Предмет: Другие предметы,
автор: Радуха5555555555
Предмет: Русский язык,
автор: golovanovmarg
Предмет: Алгебра,
автор: olyshepeleva58
Предмет: Математика,
автор: ШЕЛЧОК