Предмет: Математика,
автор: arturgurinovich228
Найдите частное решение линейного дифференциального уравнения:
Приложения:
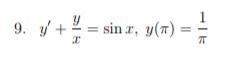
Ответы
Автор ответа:
0
Находим частное решение, подставляя начальные условия
— частное решение
Похожие вопросы
Предмет: Русский язык,
автор: kkrdyumov
Предмет: Қазақ тiлi,
автор: Bobili
Предмет: Русский язык,
автор: зигфилд
Предмет: Химия,
автор: danielagaev