Question

В треугольнике ABC угол A равен 120∘. Известно, что AB=6, а биссектриса угла A равна 4. Найдите длину стороны AC.
Решите, пожалуйста, через площади.

Answer 1

Ответ: 12 (ед. длины)

Объяснение:  

 Одна из формул биссектрисы треугольника

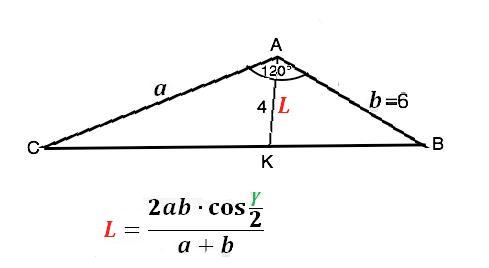
                 L={2ab•cos(0,5γ)}:(a+b) ,

где L биссектриса, а и b- стороны, γ - угол между ними.

На приведенном рисунке АК - биссектриса ∆ АВС, АС=а, АВ=6,  угол А=γ =120°

cos0,5γ=cos60°=1/2

4=2a•6•0,5/(a+6) =>

4a+24=6a =>

АС=a=12 (ед. длины)

Или с тем же результатом найти:

1) По т. косинусов из ∆ АКВ найти КВ

2) по т. синусов из ∆ АКВ угол В

3) из суммы углов треугольника угол С

4) по т. синусов вычислить длину искомой стороны АС