Предмет: Алгебра,
автор: renat027pckls3
Найдите значениt выражения
Приложения:
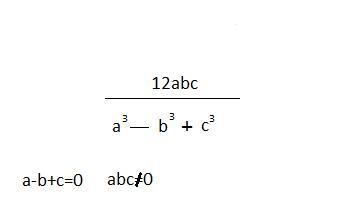
Ответы
Автор ответа:
1
Ответ:
-4
Объяснение:
Автор ответа:
1
Похожие вопросы
Предмет: Українська мова,
автор: Аноним
Предмет: Русский язык,
автор: lelen66
Предмет: Английский язык,
автор: Darja2003
Предмет: Алгебра,
автор: ГариТ0п0р
Предмет: География,
автор: ali184