Предмет: Алгебра,
автор: ryyr5tyr5
Помогите решить даю 60 баллов
Приложения:
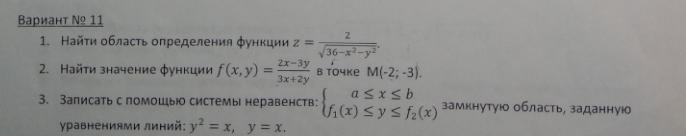
Ответы
Автор ответа:
0
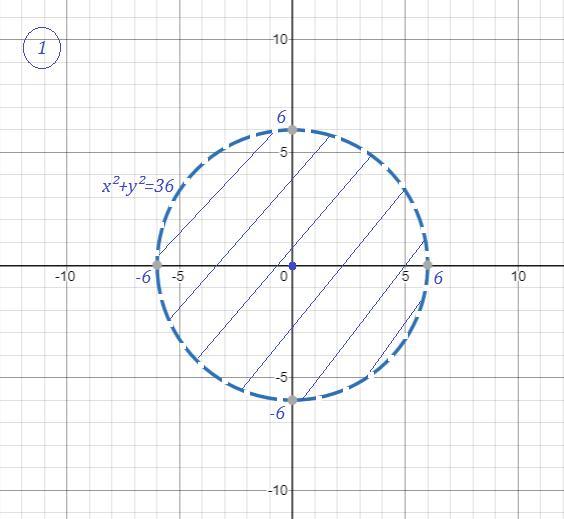
Область определения - часть плоскости, расположенная внутри окружности, уравнение которой x²+y²=36 , причём сама граница - окружность в ООФ не входит . Смотри рис.
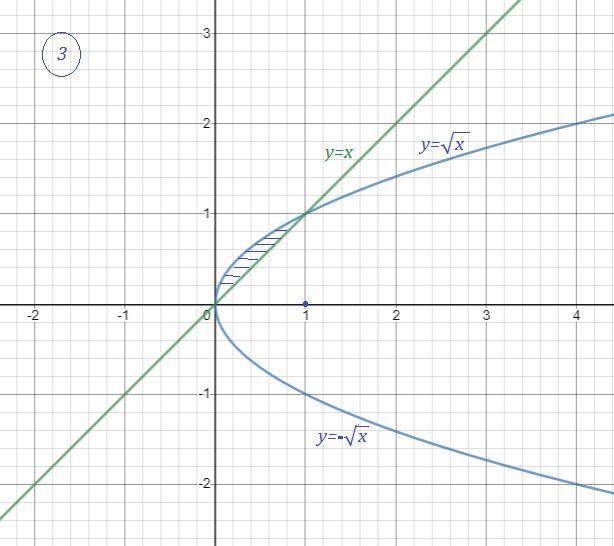
Смотри рисунок .
Приложения:
Похожие вопросы
Предмет: Беларуская мова,
автор: Seksapilb4ik
Предмет: Українська мова,
автор: Mucka
Предмет: Русский язык,
автор: gimadisla
Предмет: Геометрия,
автор: Колдокам
Предмет: Математика,
автор: УМНИКBIG