Предмет: Геометрия,
автор: arino4ka0708
Образующая конуса равна 6 см, угол при вершине осевого сечения равен 30 градусов. Найдите площадь основания конуса
Ответы
Автор ответа:
4
Дано:
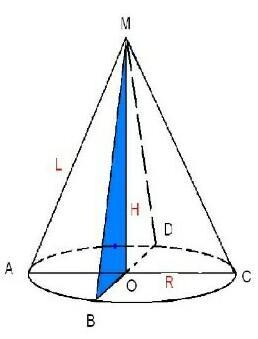
конус
l (ВМ) = 6 см (образующая)
∠ВМО = 30°
Найти:
S осн - ?
Решение:
Осевое сечение конуса (секущая проходит через ось конуса) - равнобедренный треугольник, а высота Н (МО) разделяет этот треугольник на два прямоугольных треугольника.
sin(1/2 * 30˚) = R/l
sin(15˚) = R/6
sin(45˚ - 30˚) = R/6
sin(45˚) cos(30˚) - cos(45˚) sin(30˚) = R/6
(√2/3) * (√3/2) - (√2/2) * 1/2 = R/6
(√6/4) - (√2/4) = R/6
((√6) - (√2)) * 6 = 4R
(6√6) - (6√2) = 4R
4R= 6√6 - 6√2
R = (3√6) - (3√2)/2
Итак, ВО (R) = (3√6) - (3√2)/2
S осн = пR²
S осн = п((3√6) - (3√2)/2)² = 18 - 9√3п см²
Ответ: 18 - 9√3п см²
Приложения:
Похожие вопросы
Предмет: Английский язык,
автор: 79874077725арина
Предмет: Русский язык,
автор: DrPepsi
Предмет: Английский язык,
автор: Rainbows
Предмет: Математика,
автор: Аноним
Предмет: История,
автор: LevelUP83