Предмет: Геометрия,
автор: leekyf
Два кола, радіуси яких дорівнюють R і r(r < R), дотикаються зовні. Знайдіть радіус більшого з кіл, що дотикаються до цих кіл та їхньої спільної зовнішньої дотичної.
sergyzak2020bor:
о мрак.. не вижу решения
Ответы
Автор ответа:
2
Позначимо шуканий радіус як t.
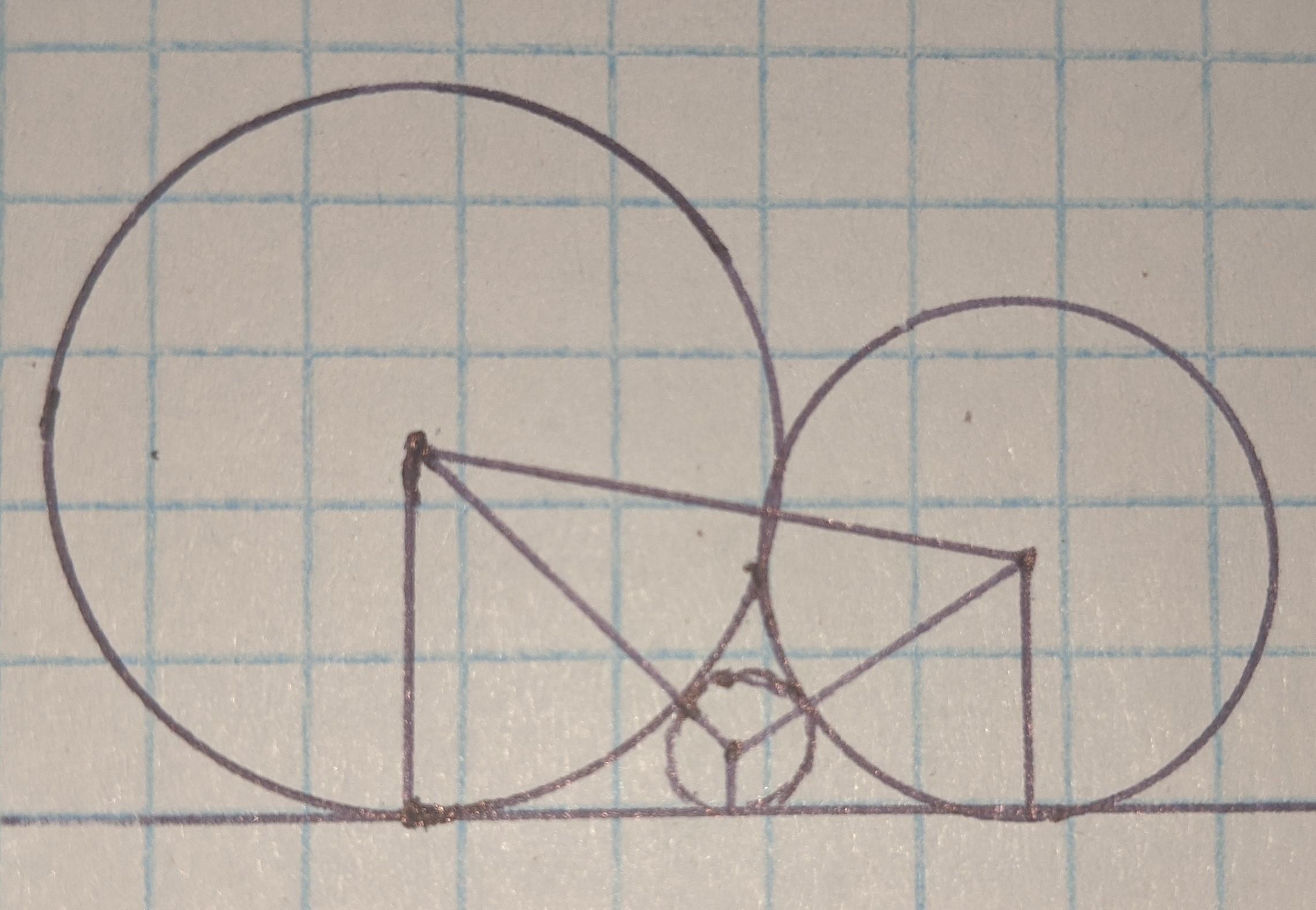
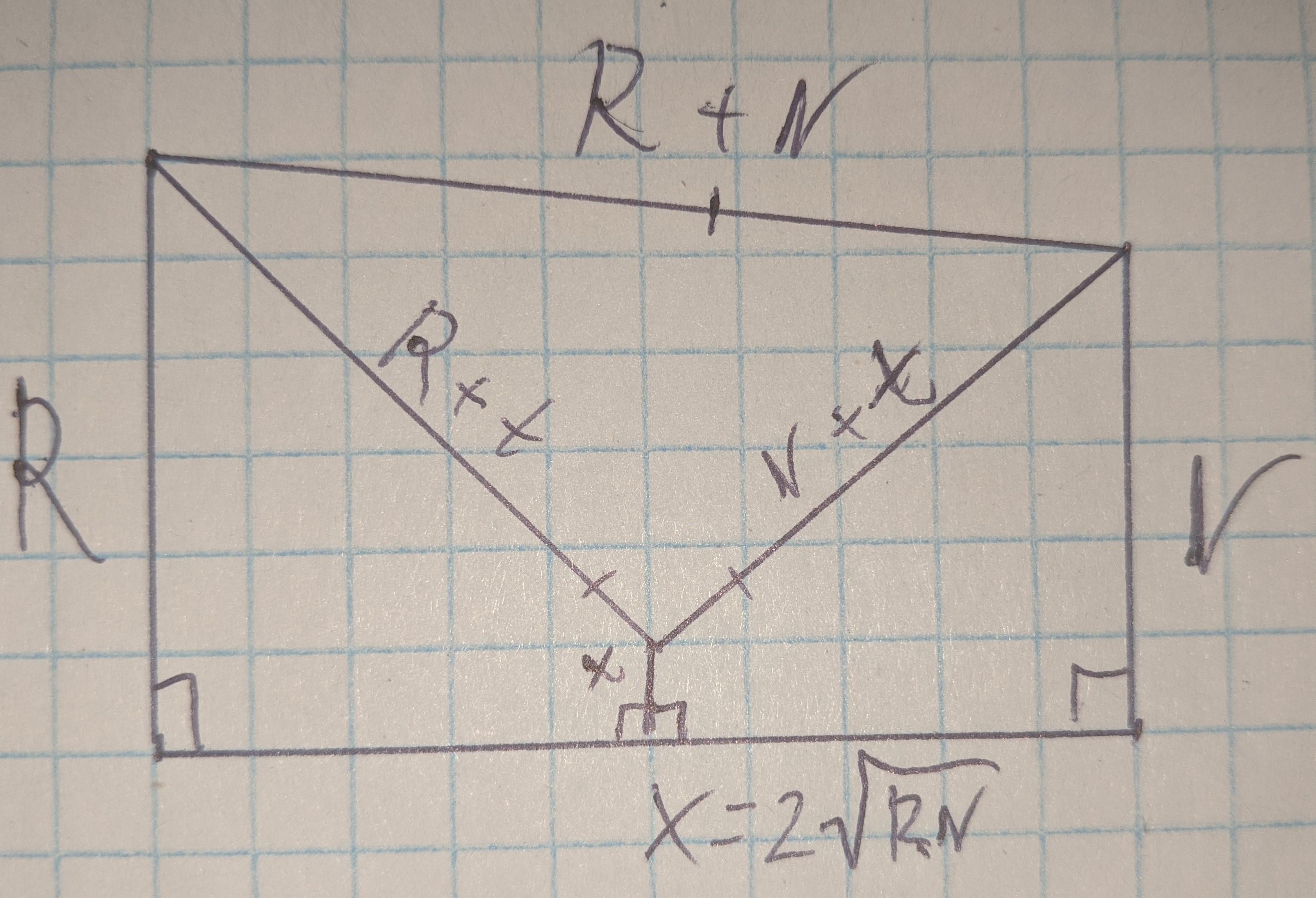
З'єднавши центри кіл, та провівши від них перпендикуляри до дотичної, отримаємо прямокутну трапецію, основи якої дорівнюють R та r, а похила бічна - R + r.
Бічна що залишилась, знаходиться з допомогою теореми Піфагора:
Всередині основної трапеції, є дві менших, з основами R і t, та r і t. Їх похилі, відповідно рівні R + t та r + t.
Тепер використовуючи все ту ж теорему Піфагора, зіставляємо рівняння:
Ось і наш радіус.
Приложения:
а причесать это все? R то ладно. r почемуто N стало Если искомый радиус х, то что за R+t, N+t, t=x так тогда сразу х и можно было б писать, но это я придираюсь =)
Похожие вопросы
Предмет: Русский язык,
автор: макни
Предмет: Английский язык,
автор: Nashua1999
Предмет: Українська мова,
автор: aleksandrostap
Предмет: Математика,
автор: Smvn
Предмет: Математика,
автор: Norins